Formation à l'examen : circuits série et parallèles - Radio-Club de Viry-Châtillon (91)

Formation à l’examen : circuits série et parallèles

par F5FOD, Jean-Pierre Waymel

1. Loi des nœuds
Un « nœud » est le point commun de connexion électrique de plusieurs éléments : fils, composants, cosses, etc. Dans le schéma ci-dessous, le point A est un nœud :

La loi des nœuds s'écrit de la façon suivante :
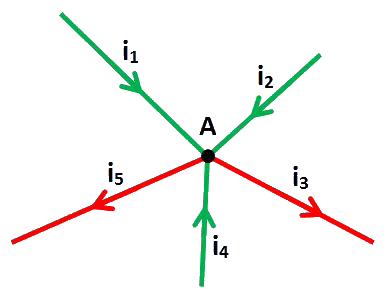
« La somme des courants entrants est égale à la somme des courants sortants ».
Soit, dans notre exemple :

$\boldsymbol{{{i}_{1}}+{{i}_{2}}+{{i}_{4}}={{i}_{3}}+{{i}_{5}}}$

2. Résistances en série et en parallèle
2.1 Structures d'un circuit série et d'un circuit parallèle
Prenons 3 résistances R1, R2 et R3 et un générateur Géné :

En série :
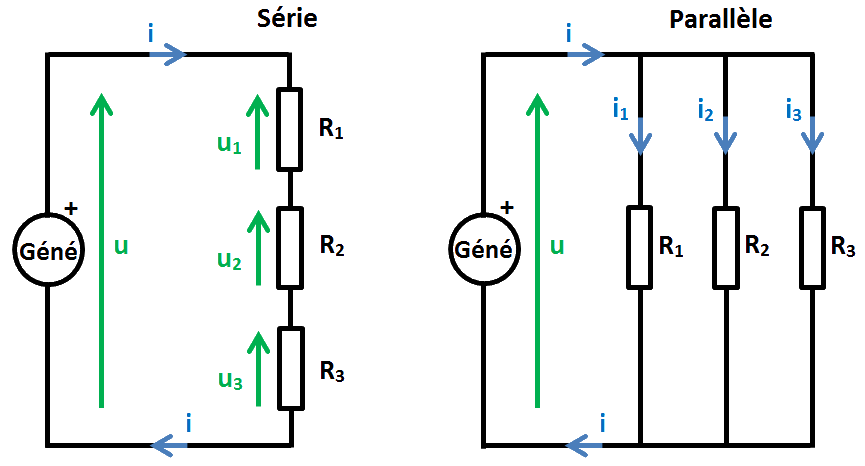
- un même courant i traverse chaque résistance R1, R2 et R3,
- les tensions u1, u2 et u3 s'ajoutent.

En parallèle :
- une même tension u est présente aux bornes de chaque résistance R1, R2 et R3,
- les courants i1, i2 et i3 suivent la loi des nœuds.

Si le générateur est un générateur de tension continue, la ou les tensions aux bornes des résistances et le ou les courants les traversant sont des tensions et des courants continus.
Si le générateur est un générateur de tension sinusoïdale, nous considèrerons leurs valeurs efficaces.
Dans le cas présent des résistances, il pourra s'agir aussi de leurs valeurs instantanées car tensions et courants sont en phase.

2.2 Appliquons la loi d'Ohm

$\boldsymbol{u=Ri \qquad \: i=\frac{u}{R}}$

Appliquons la loi d'Ohm à chaque résistance R1, R2 et R3 :

Montage « en série »	Montage « en parallèle »
$\boldsymbol{u={{u}_{1}}+{{u}_{2}}+{{u}_{3}}}$	$\boldsymbol{i={{i}_{1}}+{{i}_{2}}+{{i}_{3}}}$
$\boldsymbol{u={{R}_{1}}i+{{R}_{2}}i+{{R}_{3}}i}$	$\boldsymbol{i={u}/{{{{R}_{1}}}}\;+{u}/{{{{R}_{2}}+}}\;{u}/{{{{R}_{3}}}}\;}$
$\boldsymbol{u=({{R}_{1}}+{{R}_{2}}+{{R}_{3}})i}$	$\boldsymbol{i=\left( {{1}/{{{{R}_{1}}}}\;+{1}/{{{{R}_{2}}}}\;+{1}/{{{{R}_{3}}}}\;} \right)u}$
$\boldsymbol{{u}/{i}\;={{R}_{1}}+{{R}_{2}}+{{R}_{3}}}$	$\boldsymbol{{i}/{u}\;={1}/{{{{R}_{1}}}}\;+{1}/{{{{R}_{2}}}}\;+{1}/{{{{R}_{3}}}}\;}$
$\boldsymbol{R={{R}_{1}}+{{R}_{2}}+{{R}_{3}}}$	$\boldsymbol{{1}/{R}\;={1}/{{{{R}_{1}}}}\;+{1}/{{{{R}_{2}}}}\;+{1}/{{{{R}_{3}}}}\;}$

2.3 La « seconde » loi d'Ohm
Appelons « conductance » G l'inverse de la valeur de la résistance R.
G s'exprime en siemens (S).
Autrefois, le « mho » était l'unité de conductance, « mho » comme « ohm » lu de droite à gauche !
Notons que le mho est encore utilisé aux États-Unis.
1 mho = 1 siemens.

Par définition de la conductance, nous obtenons :

$\boxed{\boldsymbol{G=\frac{1}{R}}}$

Introduisons G dans la loi d'Ohm :

$\boldsymbol{U=RI\Rightarrow I=\frac{U}{R}=\frac{1}{R}U=GU}$

ce qui donne la « seconde » loi d'Ohm :

$\boxed{\boldsymbol{I=GU}}$

2.4 Dualité « série » < = > « parallèle »
Pour le montage « en parallèle », utilisons les conductances

$\boldsymbol{G{}_{1}=\frac{1}{{{{R}_{1}}}} \qquad \: G{}_{2}=\frac{1}{{{{R}_{2}}}} \qquad \: G{}_{3}=\frac{1}{{{{R}_{3}}}}}$

dans notre tableau :

Montage « en série »	Montage « en parallèle »
$\boldsymbol{u={{u}_{1}}+{{u}_{2}}+{{u}_{3}}}$	$\boldsymbol{i={{i}_{1}}+{{i}_{2}}+{{i}_{3}}}$
$\boldsymbol{u={{R}_{1}}i+{{R}_{2}}i+{{R}_{3}}i}$	$\boldsymbol{i={{G}_{1}}u+{{G}_{2}}u+{{G}_{3}}u}$
$\boldsymbol{u=({{R}_{1}}+{{R}_{2}}+{{R}_{3}})i}$	$\boldsymbol{i=({{G}_{1}}+{{G}_{2}}+{{G}_{3}})u}$
$\boldsymbol{{u}/{i}\;={{R}_{1}}+{{R}_{2}}+{{R}_{3}}}$	$\boldsymbol{{i}/{u}\;={{G}_{1}}+{{G}_{2}}+{{G}_{3}}}$
$\boldsymbol{R={{R}_{1}}+{{R}_{2}}+{{R}_{3}}}$	$\boldsymbol{G={{G}_{1}}+{{G}_{2}}+{{G}_{3}}}$

Pour passer du montage « série » au montage « parallèle », nous constatons qu'il suffit de changer :
u en i
i en u
R en G
… et réciproquement !

2.5 Résistances en série et en parallèle : résumé
En série : les résistances s'ajoutent.
En parallèle : les conductances s'ajoutent… ou les inverses des résistances s'ajoutent pour obtenir… l'inverse de la résistance équivalente !

3. Bobines en série et en parallèle
3.1 Impédance d'une bobine
Soit une bobine L d'inductance L, en henrys.
L'impédance XL d'une bobine est en quelque sorte l'équivalent d'une résistance MAIS ce n'est pas une résistance car - contrairement au cas de la résistance - la tension aux bornes d'une bobine n'est pas en phase avec le courant qui la traverse.
Dans le cas qui nous intéresse ici, la bobine est considérée comme parfaite. Cette tension est alors en quadrature avance par rapport à ce courant.
Néanmoins cette impédance s'exprime en ohms et se formule de la façon suivante :

$\boxed{\boldsymbol{{{X}_{L}}=L\omega}}$

où ω est la pulsation du signal fourni par le générateur si ce dernier est un générateur de tension sinusoïdale de fréquence F, avec

$\boldsymbol{\omega =2\pi F}$

En fait d'impédance, on devrait dire « module d'impédance » mais l'utilisation des nombres complexes n'est pas au programme de l'examen.
Ce module d'impédance est également appelé « réactance inductive ».

Point fondamental
Cette réactance ne dépend pas que de la bobine elle-même, elle dépend également de la fréquence F du signal sinusoïdal qui lui est appliqué :

$\boxed{\boldsymbol{{{X}_{L}}=L\omega =2\pi FL}}$

3.2 Appliquons la loi d'Ohm
Remplaçons maintenant nos 3 résistances R1, R2 et R3 par 3 bobines L1, L2 et L3.
Ces bobines seront suffisamment éloignées les unes des autres (nous en verrons plus tard la raison…).
Nous pouvons reprendre les tableaux utilisés pour les résistances si nous faisons appel aux valeurs efficaces des tensions et courants.
Pour une bobine, la loi d'Ohm s'exprime de la façon suivante :

$\boldsymbol{{{u}_{{eff}}}=L\omega {{i}_{{eff}}} \qquad \: {{i}_{{eff}}}=\frac{{{{u}_{{eff}}}}}{{L\omega }}}$

Appliquons la loi d'Ohm à chaque bobine L1, L2 et L3 :

Montage « en série »

$\boldsymbol{{{u}_{{eff}}}={{u}_{{1eff}}}+{{u}_{{2eff}}}+{{u}_{{3eff}}}}$

$\boldsymbol{{{u}_{{eff}}}={{L}_{1}}\omega {{i}_{{eff}}}+{{L}_{2}}\omega {{i}_{{eff}}}+{{L}_{3}}\omega {{i}_{{eff}}}}$

$\boldsymbol{{{u}_{{eff}}}=({{L}_{1}}+{{L}_{2}}+{{L}_{3}})\omega {{i}_{{eff}}}}$

$\boldsymbol{L\omega =({{L}_{1}}+{{L}_{2}}+{{L}_{3}})\omega}$

$\boldsymbol{L={{L}_{1}}+{{L}_{2}}+{{L}_{3}}}$

Montage « en parallèle »

$\boldsymbol{{{i}_{{eff}}}={{i}_{{1eff}}}+{{i}_{{2eff}}}+{{i}_{{3eff}}}}$

$\boldsymbol{{{i}_{{eff}}}={{{{u}_{{eff}}}}}/{{({{L}_{1}}\omega )+}}\;{{{{u}_{{eff}}}}}/{{({{L}_{2}}\omega )+}}\;{{{{u}_{{eff}}}}}/{{({{L}_{3}}\omega )}}\;}$

$\boldsymbol{{{i}_{{eff}}}={{(1}}/{{{{L}_{1}}+}}\;{1}/{{{{L}_{2}}+}}\;{1}/{{{{L}_{3}})}}\;({1}/{{\omega )}}\;{{u}_{{eff}}}}$

$\boldsymbol{{{(1}}/{L}\;)({1}/{{\omega )}}\;={{(1}}/{{{{L}_{1}}+}}\;{1}/{{{{L}_{2}}+}}\;{1}/{{{{L}_{3}})}}\;({1}/{{\omega )}}\;}$

$\boldsymbol{{1}/{L}\;={1}/{{{{L}_{1}}+}}\;{1}/{{{{L}_{2}}+}}\;{1}/{{{{L}_{3}}}}\;}$

3.3 Bobines en série et en parallèle : résumé
En série : les inductances s'ajoutent.
En parallèle : les inverses des inductances s'ajoutent pour obtenir l'inverse de l'inductance équivalente.

4. Condensateurs en série et en parallèle
4.1 Impédance d'un condensateur
Soit un condensateur C de capacité C, en farads.
L'impédance XC d'un condensateur est en quelque sorte l'équivalent d'une résistance MAIS ce n'est pas une résistance car - contrairement au cas de la résistance - la tension aux bornes d'un condensateur n'est pas en phase avec le courant qui le traverse.
Dans le cas qui nous intéresse ici, le condensateur est considéré comme parfait. Cette tension est alors en quadrature retard par rapport à ce courant.
Néanmoins cette impédance s'exprime en ohms et se formule de la façon suivante :

$\boxed{\boldsymbol{{{X}_{C}}=\frac{1}{{C\omega }}}}$

où ω est la pulsation du signal fourni par le générateur si ce dernier est un générateur de tension sinusoïdale de fréquence F, avec

$\boldsymbol{\omega =2\pi F}$

En fait d'impédance, on devrait dire « module d'impédance ».
Ce module d'impédance est également appelé « réactance capacitive ».

Point fondamental
Cette réactance ne dépend pas que du condensateur lui-même, elle dépend également de la fréquence F du signal sinusoïdal qui lui est appliqué :

$\boxed{\boldsymbol{{{X}_{C}}=\frac{1}{{C\omega }}=\frac{1}{{2\pi FC}}}}$

4.2 Appliquons la loi d'Ohm
Remplaçons maintenant nos 3 bobines L1, L2 et L3 par 3 condensateurs C1, C2 et C3.
Nous pouvons reprendre les tableaux utilisés pour les résistances si nous faisons appel aux valeurs efficaces des tensions et courants.
Pour un condensateur, la loi d'Ohm s'exprime de la façon suivante :

$\boldsymbol{{{u}_{{eff}}}=\frac{1}{{C\omega }}{{i}_{{eff}}} \qquad \: {{i}_{{eff}}}=C\omega {{u}_{{eff}}}}$

Appliquons la loi d'Ohm à chaque condensateur C1, C2 et C3 :

Montage « en série »

$\boldsymbol{{{u}_{{eff}}}={{u}_{{1eff}}}+{{u}_{{2eff}}}+{{u}_{{3eff}}}}$

$\boldsymbol{{{u}_{{eff}}}={{{{i}_{{eff}}}}}/{{({{C}_{1}}\omega )+}}\;{{{{i}_{{eff}}}}}/{{({{C}_{2}}\omega )+}}\;{{{{i}_{{eff}}}}}/{{({{C}_{3}}\omega )}}\;}$

$\boldsymbol{{{u}_{{eff}}}={{(1}}/{{{{C}_{1}}+}}\;{1}/{{{{C}_{2}}+}}\;{1}/{{{{C}_{3}})}}\;({1}/{{\omega )}}\;{{i}_{{eff}}}}$

$\boldsymbol{{{(1}}/{C}\;)({1}/{{\omega )}}\;={{(1}}/{{{{C}_{1}}+}}\;{1}/{{{{C}_{2}}+}}\;{1}/{{{{C}_{3}})}}\;({1}/{{\omega )}}\;}$

$\boldsymbol{{1}/{C}\;={1}/{{{{C}_{1}}+}}\;{1}/{{{{C}_{2}}+}}\;{1}/{{{{C}_{3}}}}\;}$

Montage « en parallèle »

$\boldsymbol{{{i}_{{eff}}}={{i}_{{1eff}}}+{{i}_{{2eff}}}+{{i}_{{3eff}}}}$

$\boldsymbol{{{i}_{{eff}}}={{C}_{1}}\omega {{u}_{{eff}}}+{{C}_{2}}\omega {{u}_{{eff}}}+{{C}_{3}}\omega {{u}_{{eff}}}}$

$\boldsymbol{{{i}_{{eff}}}=({{C}_{1}}+{{C}_{2}}+{{C}_{3}})\omega {{u}_{{eff}}}}$

$\boldsymbol{C\omega =({{C}_{1}}+{{C}_{2}}+{{C}_{3}})\omega}$

$\boldsymbol{C={{C}_{1}}+{{C}_{2}}+{{C}_{3}}}$

4.3 Condensateurs en série et en parallèle : résumé
En série : les inverses des capacités s'ajoutent pour obtenir l'inverse de la capacité équivalente.
En parallèle : les capacités s'ajoutent.

5. Résistances, bobines et condensateurs en série et en parallèle : résumé final

Montage « en série »	Montage « en parallèle »
$\boldsymbol{R={{R}_{1}}+{{R}_{2}}+{{R}_{3}}}$	$\boldsymbol{{1}/{R}\;={1}/{{{{R}_{1}}}}\;+{1}/{{{{R}_{2}}}}\;+{1}/{{{{R}_{3}}}}\;}$
$\boldsymbol{L={{L}_{1}}+{{L}_{2}}+{{L}_{3}}}$	$\boldsymbol{{1}/{L}\;={1}/{{{{L}_{1}}+}}\;{1}/{{{{L}_{2}}+}}\;{1}/{{{{L}_{3}}}}\;}$
$\boldsymbol{{1}/{C}\;={1}/{{{{C}_{1}}+}}\;{1}/{{{{C}_{2}}+}}\;{1}/{{{{C}_{3}}}}\;}$	$\boldsymbol{C={{C}_{1}}+{{C}_{2}}+{{C}_{3}}}$

Bonus :

Montage « en série »	Montage « en parallèle »
$\boldsymbol{R={{R}_{1}}+{{R}_{2}}+{{R}_{3}}}$	$\boldsymbol{G={{G}_{1}}+{{G}_{2}}+{{G}_{3}}}$

6. Résultat : plus grand ou plus petit que ?
En série
- la résistance équivalente est plus grande que la plus grande des résistances mises en série,
- l'inductance équivalente est plus grande que la plus grande des inductances mises en série,
- la capacité équivalente est plus petite que la plus petite des capacités mises en série.

En parallèle
- la résistance équivalente est plus petite que la plus petite des résistances mises en parallèle,
- l'inductance équivalente est plus petite que la plus petite des inductances mises en parallèle,
- la capacité équivalente est plus grande que la plus grande des capacités mises en parallèle.

7. Cas particulier : seulement 2 composants de même type
C'est-à-dire 2 résistances ou 2 bobines ou 2 condensateurs.

La seule « difficulté » concerne les résistances et les bobines en parallèle ainsi que les condensateurs en série.
Faisons le calcul pour 2 résistances R1 et R2 en parallèle :

$\boldsymbol{\frac{1}{R}=\frac{1}{{{{R}_{1}}}}+\frac{1}{{{{R}_{2}}}}=\frac{{{{R}_{2}}}}{{{{R}_{1}}{{R}_{2}}}}+\frac{{{{R}_{1}}}}{{{{R}_{2}}{{R}_{1}}}}=\frac{{{{R}_{1}}+{{R}_{2}}}}{{{{R}_{1}}{{R}_{2}}}}}$

d'où :

$\boldsymbol{R=\frac{{{{R}_{1}}{{R}_{2}}}}{{{{R}_{1}}+{{R}_{2}}}}}$

Ce qui nous permet d'établir le tableau spécifique à 2 composants de même type :

Montage « en série »	Montage « en parallèle »
$\boldsymbol{R={{R}_{1}}+{{R}_{2}}}$	$\boldsymbol{R={{{{R}_{1}}{{R}_{2}}}}/{(}\;{{R}_{1}}+{{R}_{2}})}$
$\boldsymbol{L={{L}_{1}}+{{L}_{2}}}$	$\boldsymbol{L={{{{L}_{1}}{{L}_{2}}}}/{(}\;{{L}_{1}}+{{L}_{2}})}$
$\boldsymbol{C={{{{C}_{1}}{{C}_{2}}}}/{(}\;{{C}_{1}}+{{C}_{2}})}$	$\boldsymbol{C={{C}_{1}}+{{C}_{2}}}$

8. Cas particulier : seulement 2 composants de même type et de même valeur
C'est-à-dire 2 résistances ayant la même valeur R1 par exemple ou 2 bobines ayant la même valeur L1 ou 2 condensateurs ayant la même valeur C1.

La seule « difficulté » concerne les résistances et les bobines en parallèle ainsi que les condensateurs en série.
Faisons le calcul pour 2 résistances R1 en parallèle :

$\boldsymbol{\frac{1}{R}=\frac{1}{{{{R}_{1}}}}+\frac{1}{{{{R}_{1}}}}=\frac{2}{{{{R}_{1}}}}}$

d'où :

$\boldsymbol{R=\frac{{{{R}_{1}}}}{2}}$

Ce qui nous permet d'établir le tableau spécifique à 2 composants de même type et de même valeur :

Montage « en série »	Montage « en parallèle »
$\boldsymbol{R=2{{R}_{1}}}$	$\boldsymbol{R={{{{R}_{1}}}}/{2}\;}$
$\boldsymbol{L=2{{L}_{1}}}$	$\boldsymbol{L={{{{L}_{1}}}}/{2}\;}$
$\boldsymbol{C={{{{C}_{1}}}}/{2}\;}$	$\boldsymbol{C=2{{C}_{1}}}$

9. Cas particulier : n composants de même type et de même valeur
C'est-à-dire n résistances ayant la même valeur R1 par exemple ou n bobines ayant la même valeur L1 ou n condensateurs ayant la même valeur C1, n étant un nombre entier.
Le cas « n = 2 » a été traité juste ci-dessus (section 8).

La seule « difficulté » concerne les résistances et les bobines en parallèle ainsi que les condensateurs en série.
Le tableau précédent se généralise ainsi :

Montage « en série »	Montage « en parallèle »
$\boldsymbol{R=n{{R}_{1}}}$	$\boldsymbol{R={{{{R}_{1}}}}/{n}\;}$
$\boldsymbol{L=n{{L}_{1}}}$	$\boldsymbol{L={{{{L}_{1}}}}/{n}\;}$
$\boldsymbol{C={{{{C}_{1}}}}/{n}\;}$	$\boldsymbol{C=n{{C}_{1}}}$