Radio-Club de Viry-Châtillon (91) - F5KEE

par F5FOD, Jean-Pierre Waymel

Abscisse : en temps ou en angle ?
Reprenons notre tension sinusoïdale u de période T :

L'axe vertical du graphe s'appelle « axe des ordonnées ». Ici, c'est une tension, en volts par exemple.
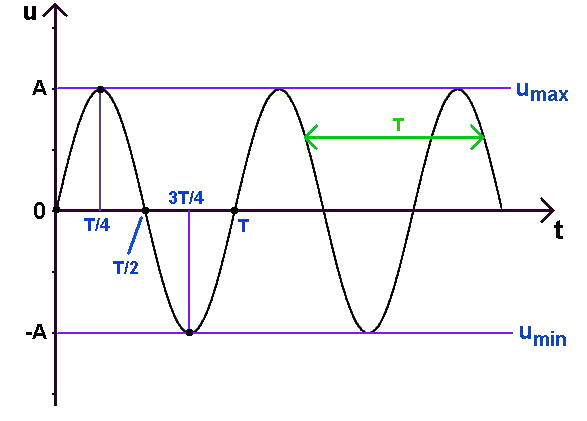
L'axe horizontal du graphe s'appelle « axe des abscisses ». Ici, c'est le temps, en secondes par exemple.
La sinusoïde représente la valeur instantanée de u, c'est-à-dire la valeur de u à tout instant t. Cette sinusoïde, comme toute sinusoïde, possède des points bien particuliers :
- les passages par 0, ici 0 volt,
- les passages par une valeur maximale, ici +A volts,
- les passages par une valeur minimale, ici −A volts. L'origine du temps t (t = 0) peut être placée où l'on veut.
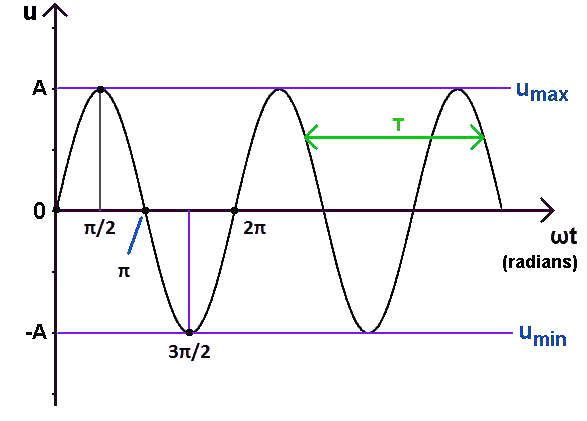
Nous pouvons aussi multiplier ce temps t par une valeur constante pour un signal sinusoïdal donné : sa pulsation ω. L'axe des abscisses sera donc gradué en valeurs d'angle puisqu'une pulsation (des radians par seconde) multipliée par un temps (des secondes) donne un angle (des radians).
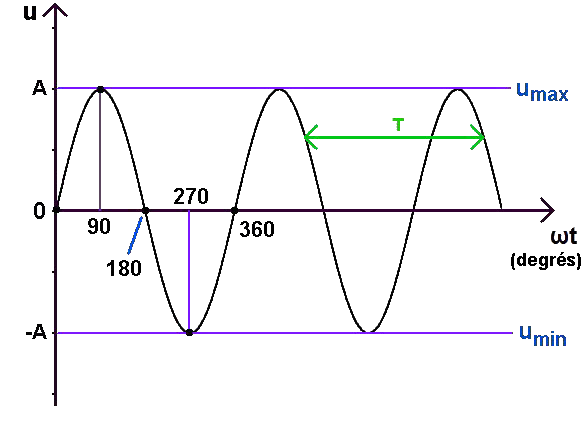
Il est bien entendu tout à fait possible de convertir les radians en degrés en se rappelant que 2π radians équivalent à 360° ou que π radians équivalent à 180°. Nous savons également que la pulsation ω et la période T sont liées par la relation suivante :

   

Ce qui nous donne :

   

et par conséquent :

   

Appliquons cette relation aux différentes valeurs particulières de t :

   

   

   

   

   

En résumé :

t	ωt en radians	ωt en degrés
0	0	0
T/4	π/2	90
T/2	π	180
3T/4	3π/2	270
T	2π	360

Nous pouvons alors graduer l'axe des abscisses non plus en temps t mais en angle ωt.
Ces angles peuvent être exprimés en radians :

ou en degrés :

Déphasage, différence de phase
Sans entrer dans des détails mathématiques qui ne sont pas au programme, on peut considérer que « déphasage » et « différence de phase » sont synonymes.
Ceci dit, considérons deux tensions u et v différentes mais de même fréquence donc de même période T et de plus sinusoïdales :

Ces deux tensions ne passent par 0 (volt) au même instant.
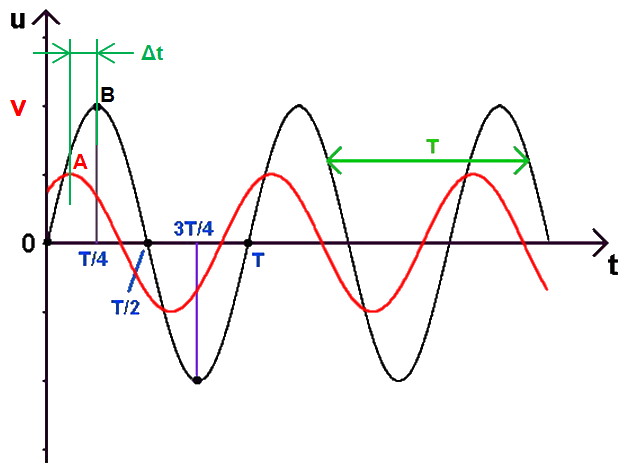
Il en est de même pour les valeurs maximales et les valeurs minimales. Par exemple, la tension v (en rouge) atteint une valeur maximale en A avant que la tension u (en noir) n'en fasse autant en B. On dit que le signal v est « en avance » par rapport au signal u… ou que signal u est « en retard » par rapport au signal v.
Cette avance (ou ce retard) dans le temps est ici nommé Δt. Cette valeur s'exprime en secondes. Sur l'axe des abscisses, nous pouvons également utiliser un angle à la place du temps, par exemple en degrés :

La signification de l'angle α sera donnée un peu plus bas.
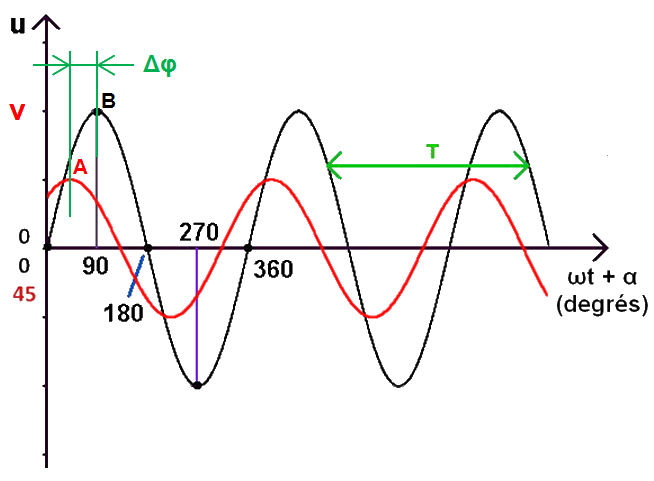
L'avance (ou le retard) est ici nommé Δφ. C'est une valeur d'angle : c'est « le déphasage », « l'angle de déphasage » ou encore « la différence de phase » entre les tensions u et v.
Le déphasage s'exprime en degrés ou en radians puisqu'il s'agit d'un angle. Dans l'exemple pris, le déphasage est égal à 45° (π/4 radian).
Comme v est en avance par rapport à u, le déphasage de v par rapport à u sera égal à +45° (+π/4 radian).
Comme u est en retard par rapport à v, le déphasage de u par rapport à v sera égal à −45° (−π/4 radian). L'énorme avantage d'exprimer le déphasage en valeur d'angle (en degrés ou en radians) est que cette valeur ne dépendra pas de la période du signal ni donc de sa fréquence !

La machine tournante
Reprenons la machine tournante qui nous avait permis de fabriquer un signal sinusoïdal :

Le point C tourne sur le cercle dans le sens conventionnel, c'est-à-dire dans le sens contraire des aiguilles d'une montre, à une vitesse égale à ω radians par seconde.
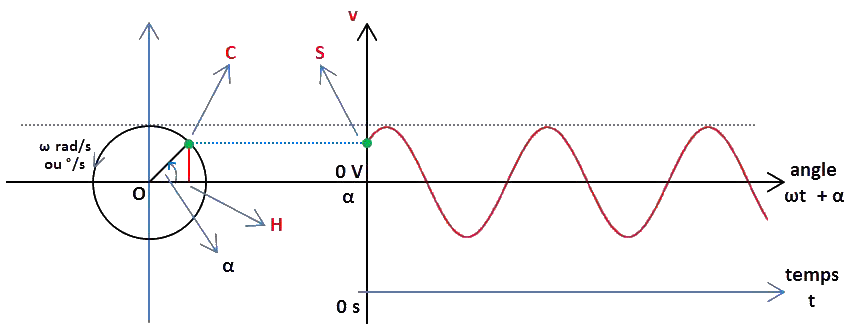
À t = 0, ce point C occupe l'emplacement indiqué sur la figure ci-dessus.
Dans notre exemple, l'angle α est égal à 45° (π/4 radian).
L'amplitude de la tension v est représentée par la longueur du segment HC, comptée positivement lors du voyage de C sur le demi-cercle « du haut » et négativement sur le demi-cercle « du bas », ces deux demi-cercles étant séparés par la ligne horizontale. Sur le graphe de droite, l'axe du temps nous permet de calculer à chaque instant t la valeur de l'angle ωt + α à reporter sur l'axe de l'angle… ωt + α. Voyons le cas t = 0 :

   

La tension v démarre donc en S, avec un angle ωt + α égal à α et une amplitude non nulle (la longueur HC). L'angle α est également appelé « phase à l'origine »… du temps (t = 0) mais il conserve bien entendu la même valeur quand le temps s'écoule ! En ce qui concerne la tension u, l'angle α est égal à 0° (0 radian). À t = 0, le point C correspondant se trouve donc sur l'axe horizontal et l'amplitude de u est nulle.
Le graphe de la tension u est alors celui dessiné sur les figures précédentes.

Hors programme… mais tellement pratique !
La tension v est entièrement décrite dans son expression mathématique :

   

Ce qui est « à l'intérieur » du sinus, c'est-à-dire ωt + α, s'appelle « la phase » de v.
Pour t = 0, voici la valeur de la phase à l'origine :

   

et la valeur de v :

   

Dans notre exemple, α est égal à 45° (π/4 radian). D'où la valeur de v pour t = 0 :

   

De même pour u :

   

Ce qui est « à l'intérieur » du sinus, c'est-à-dire ωt , est la phase de u.
Pour t = 0, voici la valeur de la phase à l'origine :

   

et la valeur de u :

   

Le déphasage de v par rapport à u, c'est-à-dire Δφ, est tout simplement la différence entre la phase de v et celle de u :

   

Et le déphasage de u par rapport à v est la différence entre la phase de u et celle de v :

   

Quand la différence est positive, il s'agit d'une avance de phase.
Quand la différence est négative, il s'agit d'un retard de phase.

Trois valeurs remarquables de déphasage
Cette fois-ci, nous allons prendre une tension u et un courant i. 1. Déphasage nul : signaux en phase

La tension u et le courant i :
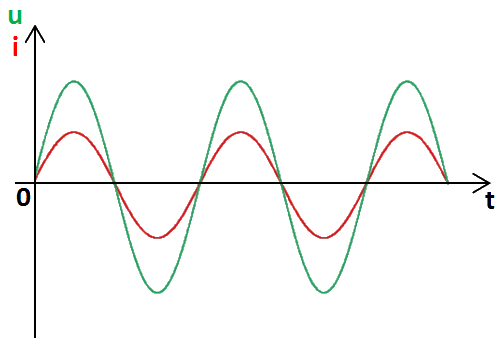
- passent par 0 (volt et ampère) au même instant,
- passent par leur valeur maximale au même instant,
- passent par leur valeur minimale au même instant. Ils sont parfaitement synchrones.
Le déphasage entre u et i est égal à 0 seconde (ou 0° ou 0 radian).
La tension u et le courant i sont « en phase ».

2. Déphasage égal à 90° (π/2 radian) : signaux en quadrature

La tension u passe par 0 (volt) quand le courant i passe par sa valeur maximale.
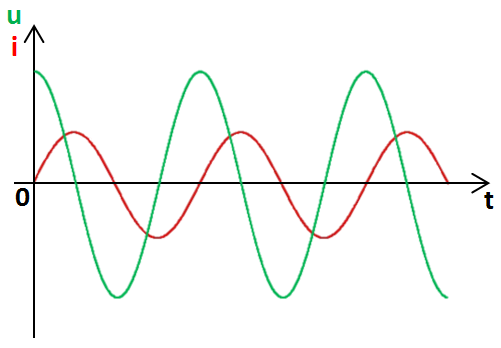
La tension u passe par 0 (volt) quand le courant i passe par sa valeur minimale.
La tension u passe par sa valeur maximale ou sa valeur minimale quand le courant i passe par 0 (ampère). Le déphasage de u par rapport à i est égal à +T/4 (ou +90° ou +π/2 radian).
Le déphasage de i par rapport à u est égal à −T/4 (ou −90° ou −π/2 radian).
La tension u est en « quadrature avance » par rapport au courant i.
Le courant i est en « quadrature retard » par rapport à la tension u.

3. Déphasage égal à 180° (π radians) : signaux en opposition de phase

La tension u et le courant i passent par 0 (volt et ampère) au même instant.
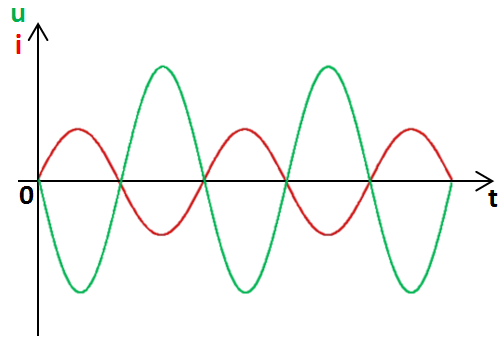
La tension u passe par sa valeur maximale quand le courant i passe par sa valeur minimale.
La tension u passe par sa valeur minimale quand le courant i passe par sa valeur maximale.
Le déphasage de i par rapport à u est égal à +T/2 (ou +180° ou +π radians).
Le déphasage de u par rapport à i est égal à −T/2 (ou −180° ou −π radians).
La tension u et le courant i sont « en opposition de phase ».

 << Causerie précédente Causerie suivante >>  << Retour à la table des matières