Formation à l'examen : filtre RL passe-bas - Radio-Club de Viry-Châtillon (91)

Formation à l’examen : filtre RL passe-bas

par F5FOD, Jean-Pierre Waymel

1. Un circuit simple : une bobine L et une résistance R
Nous allons étudier le fonctionnement du circuit suivant :

Appliquons à l'entrée de ce montage un signal sinusoïdal de fréquence F et de tension maximale e.
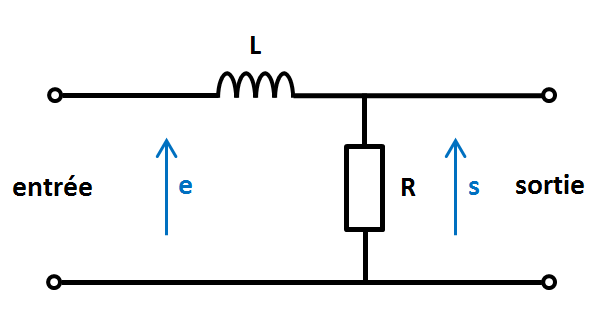
À la sortie, nous obtiendrons également un signal sinusoïdal, de même fréquence F… mais de tension maximale s pas forcément égale à e.
Nous allons étudier la variation de cette tension maximale de sortie s ou plus exactement la variation du rapport s / e en fonction de la fréquence F du signal appliqué à l'entrée.

1.1 Quand la fréquence F du signal appliqué à l'entrée est « très grande »
En elle-même l'expression « très grande » ne veut pas dire grand-chose, nous affinerons un peu plus tard !
Rappelons que l'impédance (on devrait dire « le module de l'impédance ») ZL de la bobine L se calcule de la façon suivante :

$\boxed{\boldsymbol{{{Z}_{L}}=L\omega =L\times 2\pi F=2\pi FL}}$

Si F est « très grande », ZL sera donc « très grande ». En poussant les choses à l'extrême, nous pourrons même considérer que ZL aura une valeur proche de l'infini. Autrement dit, la bobine L deviendra pratiquement un circuit ouvert.
Et comme cette bobine est en série entre l'entrée et la sortie, le signal en sortie sera quasiment nul.
Par conséquent :

(1) $\begin{equation*} \boldsymbol{s\sim 0\Rightarrow {{G}_{u}}=\frac{s}{e}\sim \frac{0}{e}=0\Rightarrow {{G}_{u}}\sim 0} \end{equation*}$

En résumé : le gain Gu sera presque égal à 0, sa valeur minimale.

1.2 Quand la fréquence F du signal appliqué à l'entrée est « très petite »
Ici aussi, l'expression « très petite » ne veut pas dire grand-chose… pour l'instant.
Si F est « très petite », ZL sera donc « très petite ». De nouveau, en poussant les choses à l'extrême, nous pourrons même considérer que ZL aura une valeur proche de 0 ohm. Autrement dit, la bobine L deviendra pratiquement un court-circuit.
Et comme cette bobine est toujours en série entre l'entrée et la sortie, le signal en sortie sera quasiment identique au signal appliqué à l'entrée.
Par conséquent :

(2) $\begin{equation*} \boldsymbol{s\sim e\Rightarrow {{G}_{u}}=\frac{s}{e}\sim \frac{e}{e}=1\Rightarrow {{G}_{u}}\sim 1} \end{equation*}$

En résumé : le gain Gu sera presque égal à 1, sa valeur maximale.

1.3 Premières conclusions
Sans effectuer de calculs, nous pouvons donc déjà affirmer que le circuit considéré :
- « laisse passer » plus facilement les signaux dont les fréquences sont « très petites » donc « très basses »,
- atténue les signaux dont les fréquences sont « très grandes » donc « très hautes ».

Très logiquement, ce circuit est appelé filtre « passe-bas ».
Bien entendu, les choses ne sont pas si simples ou du moins pas si tranchées…

2. Quand la fréquence F du signal appliqué à l'entrée n'est ni « très grande » ni « très petite »
2.1 Une formule compliquée, en apparence
Pour savoir comment réagit notre montage quand la fréquence F n'est ni « très grande » ni « très petite », il faut procéder au calcul du gain. En voici le résultat :

(3) $\begin{equation*} \boldsymbol{{{G}_{u}}=\frac{s}{e}=\frac{1}{{\sqrt{{1+{{{\left( {F/{{F}_{C}}\ } \right)}}^{2}}}}}}} \end{equation*}$

Rappelons que s et e sont les valeurs maximales des tensions sinusoïdales correspondantes.

Pas de panique, cette formule n'est pas à retenir (elle n'est pas au programme de l'examen) ! Elle va juste nous servir :
- à introduire la notion de « fréquence de coupure FC »,
- à élaborer une expression beaucoup plus simple du gain.
FC : ici l'indice C n'a rien à voir avec le C du condensateur. Il s'agit de la première lettre du mot « Coupure ». Cette fréquence spécifique se calcule de la façon suivante :

(4) $\begin{equation*} \boxed{\boldsymbol{{{F}_{C}}=\frac{R}{{2\pi L}}}} \end{equation*}$

Pour une valeur donnée de la résistance R et une valeur donnée de la bobine L cette fréquence est un paramètre fixe du montage.
Pourquoi cette fréquence est-elle appelée « fréquence de coupure » ?
Parce qu'elle délimite deux domaines de fréquences aux comportements très différents :
- un domaine où les fréquences sont inférieures à cette fréquence de coupure,
- un domaine où les fréquences sont supérieures à cette fréquence de coupure.

Exemple numérique
L = 5 H
R = 1 kΩ
FC = 32 Hz (valeur arrondie)

Remarque
Filtre RL passe-bas et filtre RL passe-haut : même expression (4) donc même fréquence de coupure FC !

2.2 Quand la fréquence F du signal appliqué à l'entrée est très grande par rapport à la fréquence de coupure FC
Remarquons que l'expression « très grande » a maintenant un véritable sens parce que nous précisons « très grande »… par rapport à une référence précise !
En conséquence :

$\boldsymbol{F\gg {{F}_{C}}\Rightarrow \frac{F}{{{{F}_{C}}}}\gg 1\Rightarrow {{\left( {\frac{F}{{{{F}_{C}}}}} \right)}^{2}}\gg 1\Rightarrow 1+{{\left( {\frac{F}{{{{F}_{C}}}}} \right)}^{2}}\sim {{\left( {\frac{F}{{{{F}_{C}}}}} \right)}^{2}}}$

L'expression du gain se transforme alors en une autre expression beaucoup plus simple :

$\boldsymbol{{{G}_{u}}\sim \frac{{1\ }}{{\sqrt{{{{{\left( {F/{{F}_{C}}\ } \right)}}^{2}}}}}}=\frac{1}{{F/{{F}_{C}}}}\Rightarrow {{G}_{u}}\sim \frac{1}{{F/{{F}_{C}}}}}$

Par exemple, si la fréquence F est très grande, le gain est presque nul. En effet, F apparaît au dénominateur du gain. On retrouve le résultat (1) précédent.

2.3 Quand la fréquence F du signal appliqué à l'entrée est très petite par rapport à la fréquence de coupure FC
L'expression « très petite » a donc maintenant elle aussi un véritable sens.
En conséquence :

$\boldsymbol{F\ll {{F}_{C}}\Rightarrow \frac{F}{{{{F}_{C}}}}\ll 1\Rightarrow {{\left( {\frac{F}{{{{F}_{C}}}}} \right)}^{2}}\ll 1\Rightarrow 1+{{\left( {\frac{F}{{{{F}_{C}}}}} \right)}^{2}}\sim 1}$

Et le gain devient presque égal à 1 :

$\boldsymbol{{{G}_{u}}\sim \frac{1}{{\sqrt{1}}}=1\Rightarrow {{G}_{u}}\sim 1}$

On retrouve le résultat (2) précédent.

2.4 Résumé

$\boldsymbol{\frac{F}{{{{F}_{C}}}}\gg 1\Rightarrow {{G}_{u}}\sim \frac{1}{{{F}/{{{{F}_{C}}}}\;}}}$

$\boldsymbol{\frac{F}{{{{F}_{C}}}}\ll 1\Rightarrow {{G}_{u}}\sim 1}$

3. Graphe du gain en tension « idéalisé » en fonction de la fréquence F du signal appliqué à l'entrée
Gain en tension « idéalisé » ? Pour ce faire, nous allons extrapoler les résultats précédents de la façon suivante :

(5) $\begin{equation*} \boldsymbol{\frac{F}{{{{F}_{C}}}}\ge 1\Rightarrow {{G}_{u}}=\frac{1}{{F/{{F}_{C}}}}} \end{equation*}$

(6) $\begin{equation*} \boldsymbol{\frac{F}{{{{F}_{C}}}}\le 1\Rightarrow {{G}_{u}}=1} \end{equation*}$

Et pour que la courbe obtenue soit universelle, c'est-à-dire valable pour toutes valeurs de la résistance R et de la bobine L donc valable quelle que soit la valeur de la fréquence de coupure FC, nous la tracerons non pas en fonction de F mais en fonction de F / FC :

Le graphe formé par le trait vert et la courbe rouge est appelé « gabarit du filtre ».
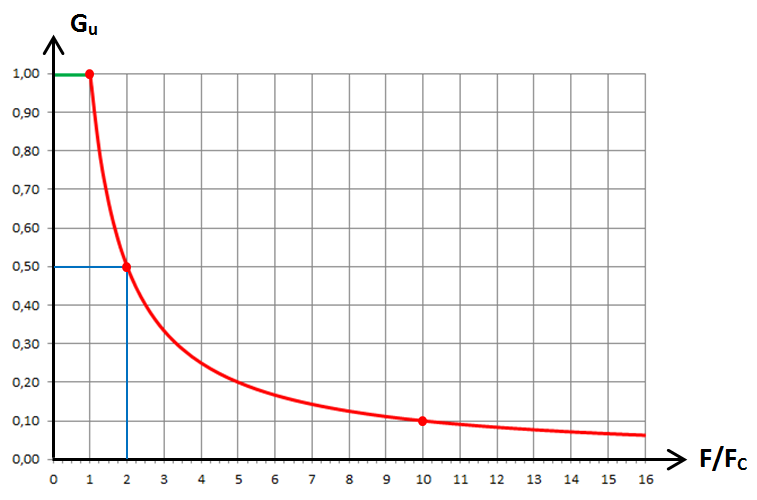
Voyons un peu plus en détails comment ce graphe a été obtenu.

3.1 Quand la fréquence F est supérieure ou égale à FC
Nous sommes ici dans le cas correspondant à l'expression (5), ce qui nous permet de tracer la courbe rouge du graphe :

$\boldsymbol{F}$	$\boldsymbol{{F}/{{{{F}_{C}}}}\;}$	$\boldsymbol{{1}/{{\left( {{F}/{{{{F}_{C}}}}\;} \right)}}\;}$	$\boldsymbol{{{G}_{u}}}$
$\boldsymbol{{{{F}_{C}}}}$	1	1	1
$\boldsymbol{2{{F}_{C}}}$	$\boldsymbol{2}$	$\boldsymbol{1/2=0,5}$	$\boldsymbol{0,5}$
$\boldsymbol{4{{F}_{C}}}$	$\boldsymbol{4}$	$\boldsymbol{1/4=0,25}$	$\boldsymbol{0,25}$
$\boldsymbol{8{{F}_{C}}}$	$\boldsymbol{8}$	$\boldsymbol{1/8=0,125}$	$\boldsymbol{0,125}$
$\boldsymbol{10{{F}_{C}}}$	$\boldsymbol{10}$	$\boldsymbol{1/10=0,1}$	$\boldsymbol{0,1}$

3.2 Quand la fréquence F est inférieure ou égale à FC
Nous sommes maintenant dans le cas correspondant à l'expression (6), ce qui nous permet de tracer le trait vert du graphe :

$\boldsymbol{F}$	$\boldsymbol{{F}/{{{{F}_{C}}}}\;}$	$\boldsymbol{{{G}_{u}}}$
$\boldsymbol{F\le {{F}_{C}}}$	$\boldsymbol{{F}/{{{{F}_{C}}\le 1}}\;}$	1

4. Graphe du vrai gain en tension en fonction de la fréquence F du signal appliqué à l'entrée
Par « vrai gain » nous entendons la valeur exacte du gain et non plus sa valeur idéalisée comme précédemment. Pour réaliser ce nouveau graphe, il suffit d'utiliser l'expression (3) pour diverses valeurs de F / FC.
En particulier, quand F est égale à FC :

$\boldsymbol{F={{F}_{C}}\Rightarrow \frac{F}{{{{F}_{C}}}}=1\Rightarrow {{G}_{u}}=\frac{1}{{\sqrt{{1+{{{\left( 1 \right)}}^{2}}}}}}=\frac{1}{{\sqrt{2}}}\sim 0,71}$

Voici ce nouveau graphe, en violet :

Le graphe du vrai gain se situe donc juste sous le gabarit (d'où ce nom de gabarit !). Il se confond d'ailleurs rapidement avec lui dès que la fréquence F dépasse 5 fois la fréquence de coupure (F / FC > 5). Il en est de même quand la fréquence F est inférieure aux deux dizièmes de la fréquence de coupure (F / FC < 0,2).

5. Graphes en décibels
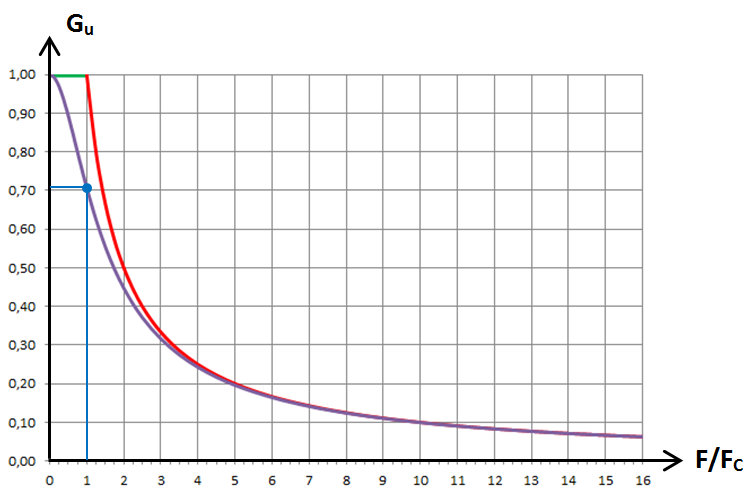
Afin de dilater le graphe pour les fréquences inférieures à FC, c-à-d quand F / FC est inférieur à 1, nous allons utiliser des échelles logarithmiques.

5.1 L'axe horizontal F / FC
L'axe horizontal est maintenant gradué selon une échelle logarithmique (logarithmes décimaux).
Les distances entre les graduations 0,01 et 0,1 puis entre 0,1 et 1 puis entre 1 et 10, etc. sont alors égales. Il n'y a pas de graduation 0 puisque la valeur log(0) n'existe pas. Cela tombe bien car cette graduation 0 correspondrait à F = 0 Hz, valeur qui ne nous intéresse pas ici…

5.2 L'axe vertical Gu
L'axe vertical reste gradué de manière classique (linéairement) mais le gain Gu est maintenant exprimé en dB (bien que l'impédance d'entrée du filtre ne soit pas égale à son impédance de sortie…) :

(7) $\begin{equation*} \boldsymbol{{{G}_{u}}\textbf{ (dB)}=20\log {{G}_{u}}} \end{equation*}$

5.3 Gabarit du filtre, en dB
Il suffit de reprendre les tableaux précédents et d'effectuer les calculs de gain en dB (revoir la causerie correspondante).

Pour la partie où F / FC est supérieur ou égal à 1, la « chute » rouge :

$\boldsymbol{F}$	$\boldsymbol{{F}/{{{{F}_{C}}}}\;}$	$\boldsymbol{{1}/{{\left( {{F}/{{{{F}_{C}}}}\;} \right)}}\;}$	$\boldsymbol{{{G}_{u}}\textbf{ en dB}}$
$\boldsymbol{{{{F}_{C}}}}$	1	1	$\boldsymbol{20\log 1=0}$
$\boldsymbol{2{{F}_{C}}}$	$\boldsymbol{2}$	$\boldsymbol{{1}/{{2}}\;=0,5}$	$\boldsymbol{20\log \left( {{{2}^{{-1}}}} \right)=-6}$
$\boldsymbol{4{{F}_{C}}}$	$\boldsymbol{4}$	$\boldsymbol{{1}/{{4}}\;=0,25}$	$\boldsymbol{20\log \left( {{{2}^{{-2}}}} \right)=-12}$
$\boldsymbol{8{{F}_{C}}}$	$\boldsymbol{8}$	$\boldsymbol{{1}/{{8}}\;=0,125}$	$\boldsymbol{20\log \left( {{{2}^{{-3}}}} \right)=-18}$
$\boldsymbol{10{{F}_{C}}}$	$\boldsymbol{10}$	$\boldsymbol{{1}/{{10}}\;=0,1}$	$\boldsymbol{20\log \left( {{{10}^{{-1}}}} \right)=-20}$

Pour la partie où F / FC est inférieur ou égal à 1, le « plateau » vert :

$\boldsymbol{F}$	$\boldsymbol{{F}/{{{{F}_{C}}}}\;}$	$\boldsymbol{{{G}_{u}}\textbf{ en dB}}$
$\boldsymbol{F\le {{F}_{C}}}$	$\boldsymbol{{F}/{{{{F}_{C}}\le 1}}\;}$	$\boldsymbol{20\log 1=0}$

5.4 Courbe du vrai gain en tension, en dB
Il suffit de reprendre l'expression (3) pour diverses valeurs de F / FC puis de convertir le gain en dB au moyen de l'expression (7).
En particulier, quand F est égale à FC :

$\boldsymbol{{{G}_{u}}\textbf{ (dB)}=20\log \left( {\frac{1}{{\sqrt{2}}}} \right)=20\log \left( {{{2}^{{{{-1}}/{2}\;}}}} \right)=-3}$$

5.5 Le nouveau graphe complet

6. Deux remarques très importantes
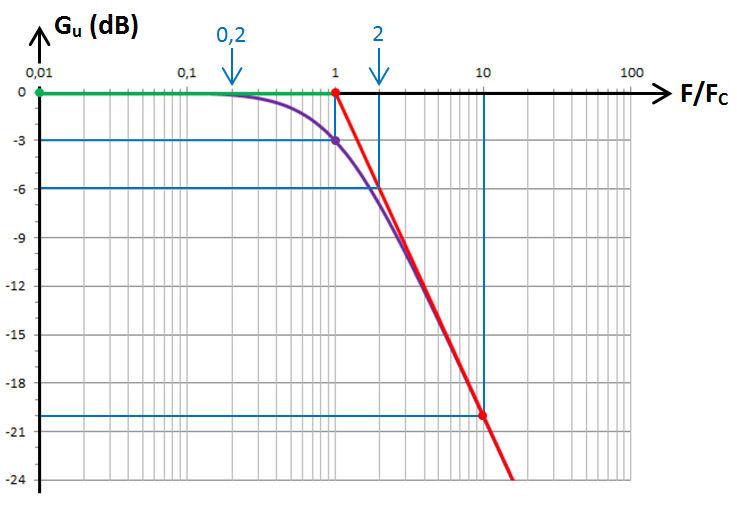
- Nous voyons que le (vrai) gain maximal frôle la valeur 1 qui correspond à 0 dB (20 × log1 = 20 × 0 = 0).
- Finalement ce (vrai) gain est toujours inférieur à 1 sans jamais vraiment atteindre 0.
Comme le logarithme d'un nombre inférieur à 1 mais toujours supérieur à 0 est négatif, l'expression du (vrai) gain en dB est ici toujours négative.

7. Ce qu'il faut retenir : les caractéristiques principales du filtre RL passe-bas
La caractéristique de base du filtre est sa fréquence de coupure FC (4).
Pour les fréquences supérieures à FC :
- le « gain gabarit » perd 6 dB à chaque fois que la fréquence est multipliée par 2, par exemple FC × 2 (−6 dB), FC × 4 (−12 dB), FC × 8 (−18 dB). Comme la bande des fréquences comprises entre une fréquence donnée et sa valeur double s'appelle « une octave », on dit que le filtre « a une pente de −6 dB par octave »,
- le « gain gabarit » perd 20 dB à chaque fois que la fréquence est multipliée par 10, par exemple à FC × 10 (−20 dB). Comme la bande des fréquences comprises entre une fréquence donnée et dix fois sa valeur s'appelle « une décade », on dit aussi que le filtre « a une pente de −20 dB par décade ».
Pour les fréquences inférieures à FC, le plateau du gabarit se situe à 0 dB.
Le « vrai gain » perd 3 dB à la fréquence de coupure FC.

8. Comment tracer rapidement le gabarit et la courbe du (vrai) gain ?
- L'expression donnant l'impédance (le module de l'impédance) d'une bobine nous informe qu'elle se comporte comme un court-circuit aux fréquences basses. Si cette bobine est placée en série entre l'entrée et la sortie du filtre, les signaux de fréquences basses vont passer facilement de l'entrée à la sortie du filtre : c'est un filtre passe-bas.

- Prendre un repère (papier ou tableur) muni d'une échelle semi-logarithmique : échelle horizontale logarithmique et échelle verticale linéaire. Tracer une droite horizontale partant du point [F / FC = 1 ; gain = 0 dB] et se dirigeant vers la gauche. Elle se confond avec une partie de l'axe horizontal.
Puis inscrire les deux points suivants : [F / FC = 1 ; gain = 0 dB] et [F / FC = 10 ; gain = −20 dB]. Tracer la droite joignant ces 2 points.
Ces deux droites forment le gabarit du filtre.

- Repérer le point [F / FC = 1 ; gain = −3 dB] : c'est un point de la courbe du (vrai) gain. Le reste de cette courbe se confond rapidement avec les droites du gabarit.

9. Relation entre pulsation de coupure et constante de temps
La pulsation de coupure ωC s'exprime de la façon suivante :

$\boldsymbol{{{\omega }_{C}}=2\pi {{F}_{C}}}$

Remplaçons FC par son expression définie en (4) :

$\boldsymbol{{{\omega }_{C}}=2\pi \frac{R}{{2\pi L}}=\frac{R}{L}}$

Rappelons maintenant l'expression de la constante de temps τ (tau) étudiée lors de la connexion d'un circuit RL à une source de tension continue :

$\boldsymbol{\tau =\frac{L}{R}}$

Nous en déduisons :

$\boxed{\boldsymbol{\tau \times {{\omega }_{C}}=1}}$

ce qui constitue un moyen mnémotechnique assez simple permettant de retrouver l'expression de la pulsation de coupure puis de la fréquence de coupure à partir de l'expression de la constante de temps.

<< Causerie précédente Causerie suivante >>

<< Retour à la table des matières

Radio-Club de Viry-Châtillon (91) - F5KEE

Nos activités autour de la radio, des techniques et des sciences, explorant et développant diverses activités et projets connexes.

Formation à l’examen : filtre RL passe-bas

Recherche

Traducteur

QSL 91

Logo F5KEE

Catégories

Contact ARISS : La Norville – F5KEE

Météo de Viry-Châtillon

Brocantes et Manifestations

Activités solaires

DX FUN Web Cluster

Listes qui suivent @f5kee

Publications récentes

Commentaires récents

Archive

Viry-Châtillon (91)

Méta

Statistiques XITI