Radio-Club de Viry-Châtillon (91) - F5KEE

par F5FOD, Jean-Pierre Waymel

Principe de base
La tension fournie par un ensemble de générateurs de tension connectés en série est égale à la somme des tensions de chacun d'entre eux.
En plus court : les tensions s'ajoutent ! Mais pas n'importe comment…
Nous allons donc détailler cette loi grâce à quelques exemples classiques.
Dans ces exemples, nous ne prendrons que deux générateurs de tension. Mais ce qui sera dit pour ces deux générateurs sera également valable pour un nombre quelconque de générateurs.

Groupement série de générateurs de tension CC
Branchement classique
Prenons deux piles parfaites P1 et P2 et connectons-les de la façon suivante :

C'est-à-dire en reliant le pôle « + » de P1 au pôle « − » de P2.
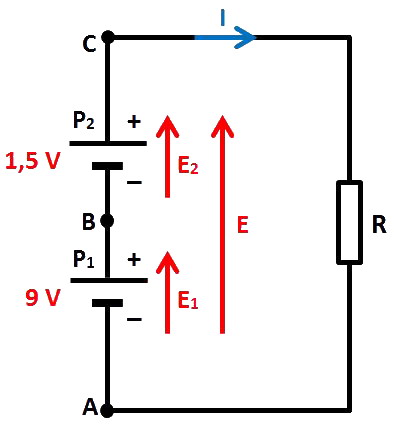
E1 est la f.é.m. de P1 et E2 celle de P2.
La f.é.m. totale E se calcule ainsi :

   

Prenons un cas concret : E1 = 9 V et E2 = 1,5 V.
E = 9 + 1,5 = 10,5 V. En utilisant l'analogie « dénivellation », on part de A puis on monte jusqu'à B et on continue de monter jusqu'à C : les dénivellations correspondantes E1 et E2 s'ajoutent pour obtenir la dénivellation totale de A à C.
Nous pouvons aussi écrire :

   

Le courant I qui circule dans le circuit va bien du « − » au « + » à l'intérieur de chaque générateur de tension, ce qui correspond au sens normal.

Branchement en opposition
Cette fois-ci, inversons le branchement de la pile P2 :

c'est-à-dire en reliant le pôle « + » de P1 au pôle « + » de P2.
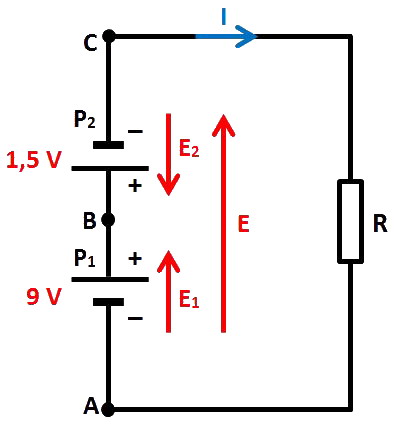
La f.é.m. totale E se calcule ainsi :

   

Nous pouvons aussi exprimer E de la façon suivante :

   

Nous retrouvons donc la même loi d'addition des tensions (ici des f.é.m.) mais il faut faire bien attention au sens de branchement des piles afin d'assigner le signe correct à chacune des tensions. Dans notre cas concret : E = 9 + (−1,5) = 9 − 1,5 = 7,5 V. Le courant I qui circule dans le circuit va bien du « − » au « + » à l'intérieur de P1, le générateur ayant la tension (f.é.m.) la plus grande, ce qui correspond au sens normal. Mais il va du « + » au  « − » à l'intérieur de P2, le générateur ayant la tension (f.é.m.) la plus petite, ce qui correspond au sens contraire au sens normal : cette pile ne va pas apprécier…

Groupement série d'un générateur de tension CC et d'un générateur de tension CA
Ce qui sera dit sur un générateur de tension CA sera également valable pour tout générateur d'une tension variable de forme quelconque. Voici le schéma d'un tel groupement :

P est une pile dont la f.é.m. est égale à E.
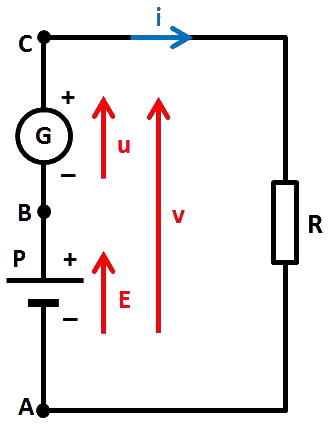
G est un générateur de tension CA, par exemple une tension sinusoïdale. La tension u fournie par G (entre C et B) peut être positive à un instant donné et négative à un autre instant. Il faudrait donc dessiner deux schémas, un pour chacun de ces deux cas.
Afin d'alléger la représentation, on utilise les notations suivantes :
- les signes « + » et « − » de G et la flèche correspondante u représentés sur le schéma correspondent au cas où la tension de C par rapport à B est positive ;
- la valeur u de la tension du générateur contient le signe « + » quand la tension de C par rapport à B est positive et le signe « − » quand la tension de C par rapport à B est négative. La tension totale v est donnée par la formule suivante :

   

Il s'agit donc toujours de la somme des tensions des générateurs connectés en série.
Ici, E a une valeur constante tandis que u et par conséquent v varient dans le temps. À nouveau, prenons un exemple concret :

Ici E = 3 V, en noir.
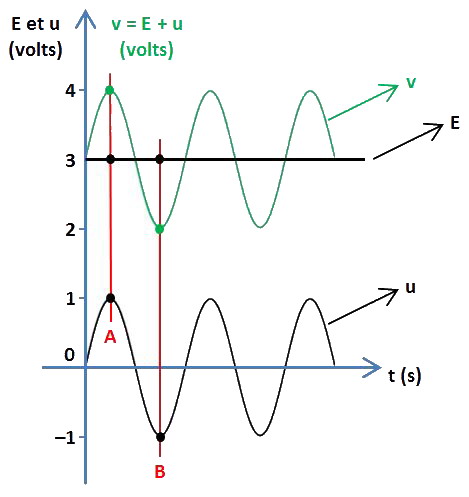
La tension sinusoïdale u, en noir également, a une valeur maximale égale +1 V : c'est sa valeur crête.
Sa valeur minimale est égale à −1 V. La représentation graphique de la somme v = E + u s'effectue point par point de la façon suivante :
- on choisit une valeur du temps t, par exemple en A, le premier maximum de u,
- on lit la valeur de u, ici +1 V,
- on lit la valeur de E, toujours +3 V puisqu'il s'agit d'une tension continue qui ne varie pas dans le temps,
- on en fait la somme : 1 + 3 = 4 V, qui est la valeur de v pour le temps choisi, ici A. De même pour le temps B, le premier minimum de u,
- on lit la valeur de u, ici −1 V,
- on lit la valeur de E, toujours +3 V puisqu'il s'agit d'une tension continue qui ne varie pas dans le temps,
- on en fait la somme : (−1) + 3 = −1 + 3 = +2 V, qui est la valeur de v pour le temps choisi, ici B. On procède ainsi pour une période de u et on obtient la représentation graphique de la somme des tensions E et u. Si u n'était pas périodique, on se limiterait à une partie du temps, sinon la construction n'aurait pas de fin… Remarque importante pour la causerie suivante
La courbe de v en fonction du temps est tout simplement la même que celle de u en fonction du temps mais translatée verticalement vers le haut de +3 V, la valeur de E. Dans cet exemple, la tension totale v est toujours positive. D'où le sens du courant i sur le schéma.
Si la pile P avait été branchée dans l'autre sens, nous aurions eu :

   

En effet, nous considérons ici que E est toujours intrinsèquement positif comme dans l'expression « une pile de 3 V ».
La courbe de v en fonction du temps serait toujours la même que celle de u en fonction du temps mais translatée verticalement vers le bas : ce serait une sinusoïde évoluant entre −2 et −4 V.
Cette tension serait toujours négative et le sens du courant i sur le schéma devrait alors être inversé. Pour d'autres valeurs de E, la tension v pourrait être positive à certains instants et négative à d'autres. Le courant i irait alors respectivement dans un sens et dans l'autre. Dans tous les cas, la valeur crête à crête reste inchangée et égale à 2 V.

Groupement série de générateurs de tension CA
Ce qui sera dit sur un générateur de tension CA sera également valable pour tout générateur d'une tension variable de forme quelconque. Prenons de suite un exemple.
Un générateur G1 délivre une tension sinusoïdale a de fréquence F. Sa valeur crête est égale à 1 V.
La tension a évolue donc entre +1 et −1 V au cours du temps.
Un second générateur G2 délivre une tension sinusoïdale b de fréquence triple soit 3F. Sa valeur crête est égale à 0,5 V.
La tension  b évolue donc entre +0,5 V et −0,5 V au cours du temps.
Connectons ces deux générateurs en série. La tension totale u obtenue aux bornes de l'ensemble se calcule ainsi :

   

À partir de la représentation graphique des tensions a et b en fonction du temps, traçons point par point, à chaque instant t, la représentation graphique de leur somme u :

La tension obtenue n'est plus une tension sinusoïdale. Elle évolue entre +1,0758… et −1,0758… V en fonction du temps.
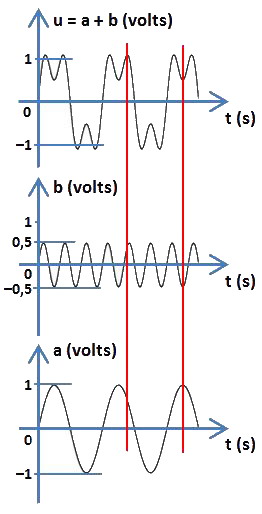
On démontre mathématiquement que cette tension est ici périodique et de fréquence F. Mais ce n'est qu'un cas particulier dépendant des choix effectués pour les tensions a et b.

Conclusion
Comme annoncé dans le principe de base en début de cette causerie, dans un branchement de générateurs de tension en série, « les tensions s'ajoutent ». Cette loi est simple mais il faut faire bien attention aux signes des tensions !

 << Causerie précédente Causerie suivante >>  << Retour à la table des matières