Formation à l’examen : modulation en Bande Latérale Unique
par F5FOD, Jean-Pierre Waymel
Se reporter à la séance précédente pour la définition des différents termes, variables ou constantes que nous allons réutiliser dans cette causerie.Nous reprendrons également les mêmes valeurs :
m = 0,3
E = 2 V
donc mE = 0,6 V 1. Rappels sur la modulation d'amplitude « classique »
1.1 Lorsque le signal utile (ou signal modulant) n'est composé que d'une seule fréquence
Modulateur
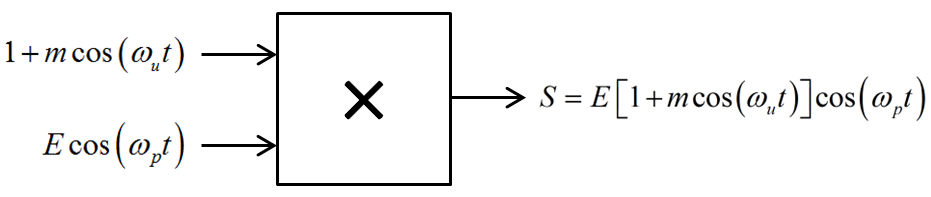
(1) ![\begin{equation*} \boxed{\boldsymbol{S=E\left[ {1+m\cos \left( {{{\omega }_{u}}t} \right)} \right]\cos \left( {{{\omega }_{p}}t} \right)=E\left[ {1+m\cos BF} \right]\cos HF}} \end{equation*}](http://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-289456bc559a6785a01b8e6aeca6bc4d_l3.png "Rendered by QuickLaTeX.com")
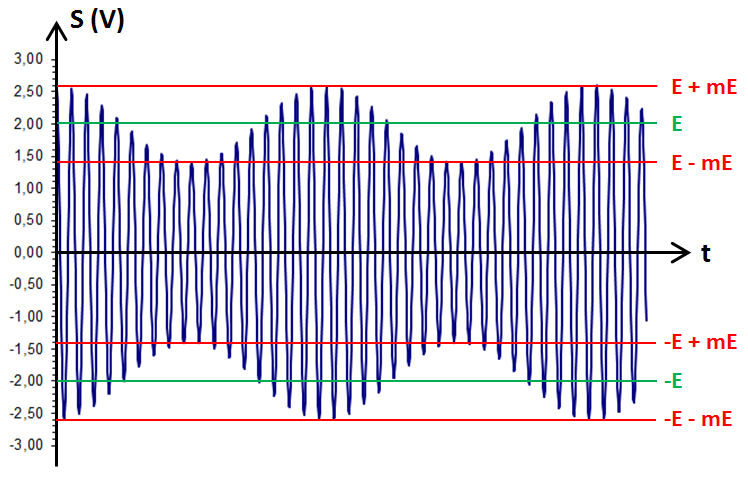
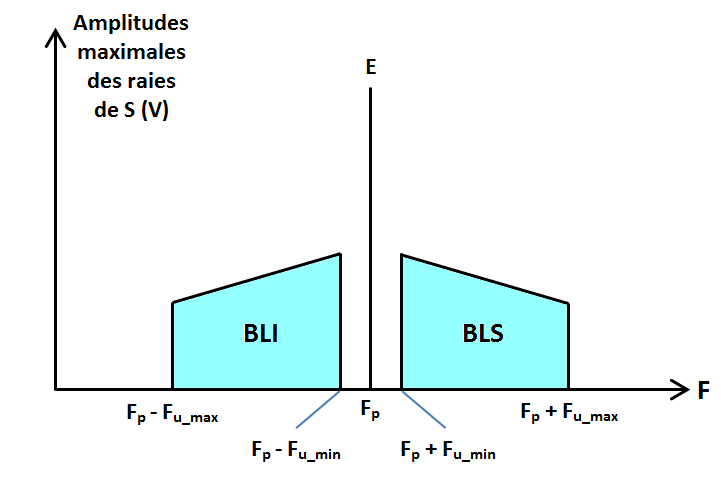
Le signal utile s’étale d’une fréquence minimale Fu_min à une fréquence maximale Fu_max.
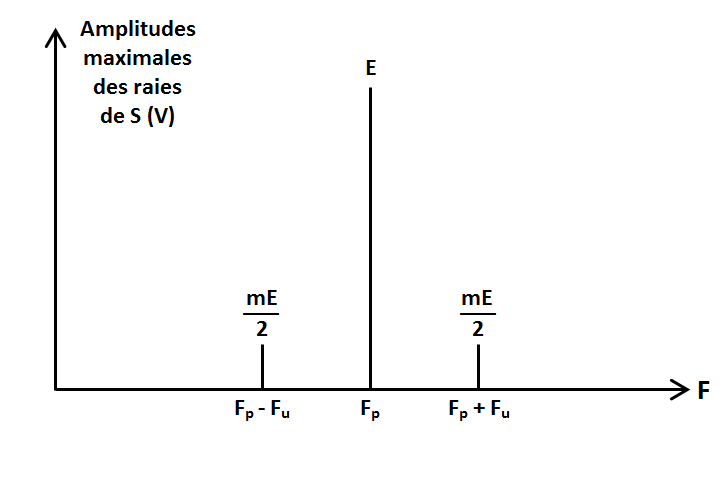
Spectre de S
Le signal S est composé :
- de la porteuse Fp et
- des deux bandes latérales BLI et BLS. La modulation d'amplitude « classique » est aussi appelée « DBAP » : Double Bande latérale Avec Porteuse (« DSB - FC », Double Side Band - Full Carrier). C'est tout simplement l'AM (Amplitude Modulation) ou le A3 d'antan… 2. Modulation d'amplitude en Double Bande latérale Sans Porteuse (DBSP)
La porteuse n’est finalement pas absolument nécessaire puisqu’elle ne contient aucune information utile. De plus elle est consommatrice d'énergie.
Supprimons-la ou plus exactement ne la rajoutons plus !
Dans l'expression (1), il suffit de retirer le « +1 » (en d'autres termes : donner une valeur nulle à l'offset).
Appelons SDBSP le signal alors obtenu, « DBSP » pour Double Bande latérale Sans Porteuse (« DSB - SC », Double Side Band - Suppressed Carrier). 2.1 Lorsque le signal utile (ou signal modulant) n'est composé que d'une seule fréquence
Modulateur
Le multiplieur est ici souvent appelé « mélangeur » (« mixer » en anglais) :
![\[ \boxed{\boldsymbol{{{S}_{{DBSP}}}=mE\cos \left( {{{\omega }_{u}}t} \right)\cos \left( {{{\omega }_{p}}t} \right)=\left( {mE\cos BF} \right)\cos HF}} \]](http://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-04a8307cff00a5e807df9994a31be4aa_l3.png "Rendered by QuickLaTeX.com")
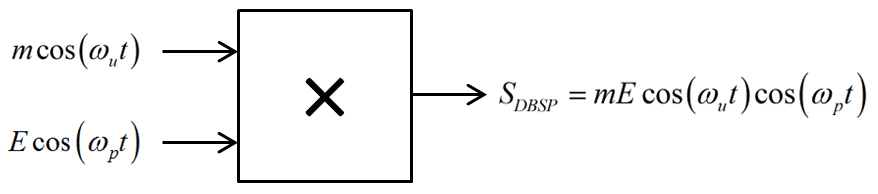
Utilisons la même méthode qu'au paragraphe 11 de la causerie précédente. L'enveloppe est ici constituée par les graphes de mEcos(ωut) et −mEcos(ωut), ce qui donne :
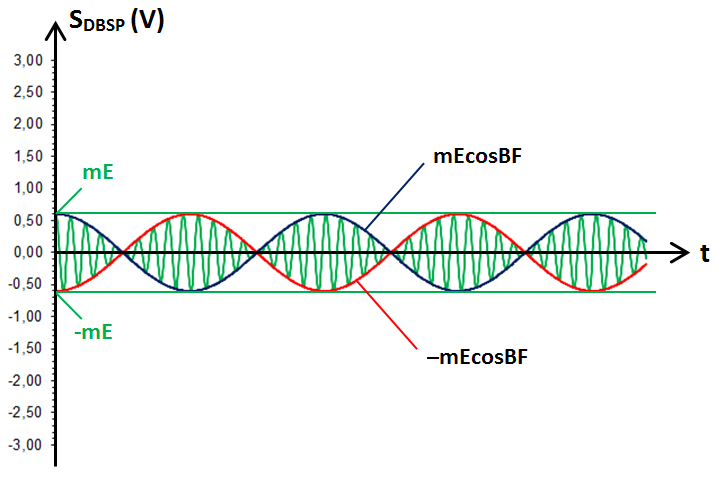
Voici le graphe réel de SDBSP :
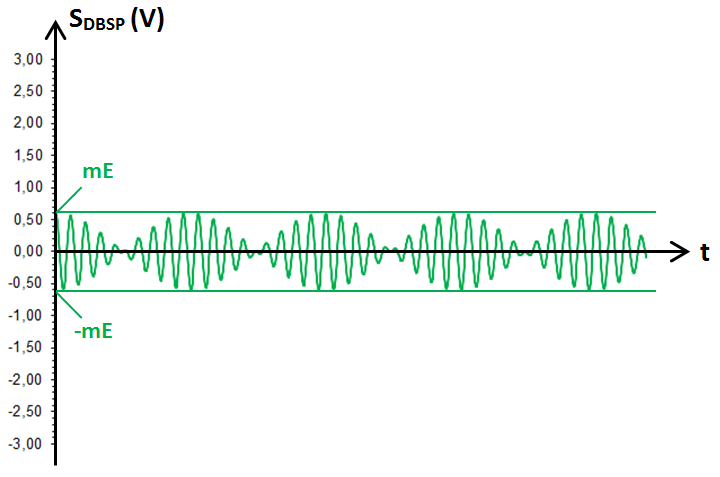
Grâce au paragraphe 5 de la causerie précédente, nous savons transformer un produit de deux cosinus en une somme :
![\[ \boxed{\boldsymbol{{{S}_{{DBSP}}}=\frac{{mE}}{2}\cos \left[ {({{\omega }_{p}}-{{\omega }_{u}})t} \right]+\frac{{mE}}{2}\cos \left[ {({{\omega }_{p}}+{{\omega }_{u}})t} \right]}} \]](http://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-ffd83d2b4eec99e20429a89bc8baba9f_l3.png "Rendered by QuickLaTeX.com")
![\[ \boxed{\boldsymbol{{{S}_{{DBSP}}}=\frac{{mE}}{2}\cos \left[ {2\pi ({{F}_{p}}-{{F}_{u}})t} \right]+\frac{{mE}}{2}\cos \left[ {2\pi ({{F}_{p}}+{{F}_{u}})t} \right]}}} \]](http://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-d1643c7179e14af3a46877da54823949_l3.png "Rendered by QuickLaTeX.com")
- un signal à la fréquence
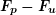et d'amplitude maximale 
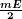, - un signal à la fréquence
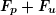et d'amplitude maximale .
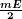Le signal utile s’étale d’une fréquence minimale Fu_min à une fréquence maximale Fu_max.
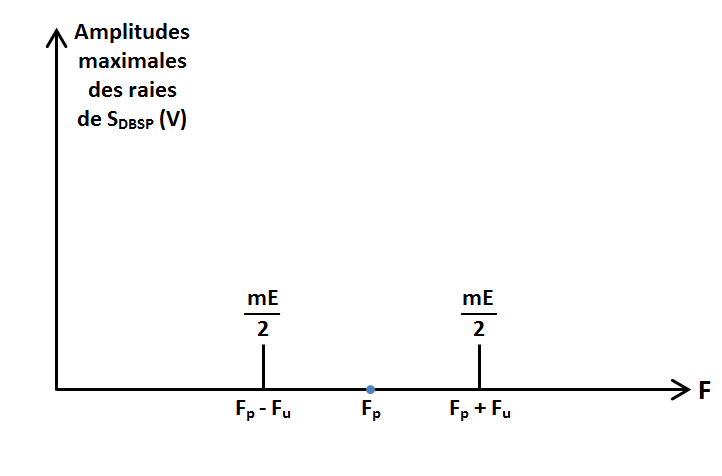
Spectre de SDBSP
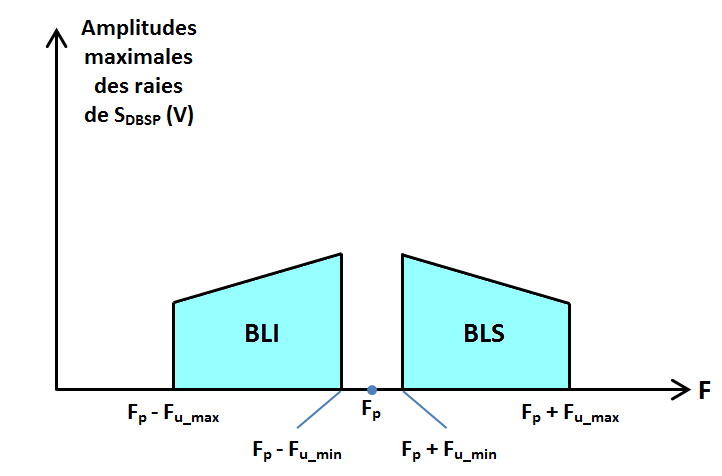
Le signal SDBSP est uniquement composé :
- des deux bandes latérales BLI et BLS. 3. Modulation d'amplitude en Bande Latérale Unique
Allons encore plus loin dans les économies ! La BLI et la BLS contiennent strictement la même information utile : il y a redondance. Supprimons donc l'une des deux bandes latérales et nous utiliserons moitié moins de spectre. Nous obtiendrons un signal modulé en « BLU », Bande Latérale Unique, sous-entendu ici sans onde porteuse (« SSB », Single Side Band, sous-entendu Suppressed Carrier).
3.1. Ajout d'un filtre passe-bande à la sortie d'un modulateur DBSP
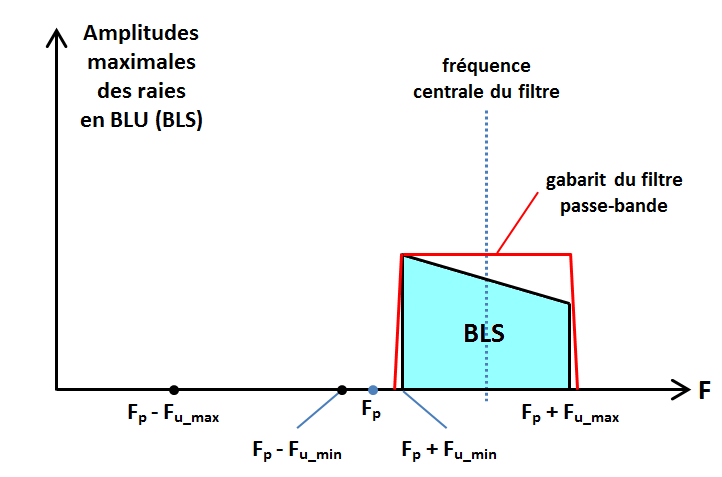
Fabriquons un filtre qui ne laisse passer que les fréquences comprises entre Fp + Fu_min et Fp + Fu_max et connectons-le à la sortie d'un modulateur Double Bande latérale Sans Porteuse (DBSP). À la sortie du filtre cette fois-ci, nous obtenons le spectre suivant :
![\[ \boldsymbol{{{F}_{{centre}}}={{F}_{p}}+\frac{{{{F}_{{u\_\min }}}+{{F}_{{u\_\max }}}}}{2}} \]](http://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-eac8a0575c2680dc66dd9155ebdb40f4_l3.png "Rendered by QuickLaTeX.com")
La BLI a maintenant disparu et il ne reste que la BLS.
L'ajout du filtre passe-bande BLS a transformé le modulateur DBSP en modulateur « BLU », Bande Latérale Unique, ici la BLS (SSB USB). Bien entendu, si le filtre est conçu de telle façon que sa fréquence centrale Fcentre tombe au milieu de la BLI, c'est-à-dire :
![\[ \boldsymbol{{{F}_{{centre}}}={{F}_{p}}-\frac{{{{F}_{{u\_\min }}}+{{F}_{{u\_\max }}}}}{2}} \]](http://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-e4423da83dd7a51332b9969903af38c3_l3.png "Rendered by QuickLaTeX.com")
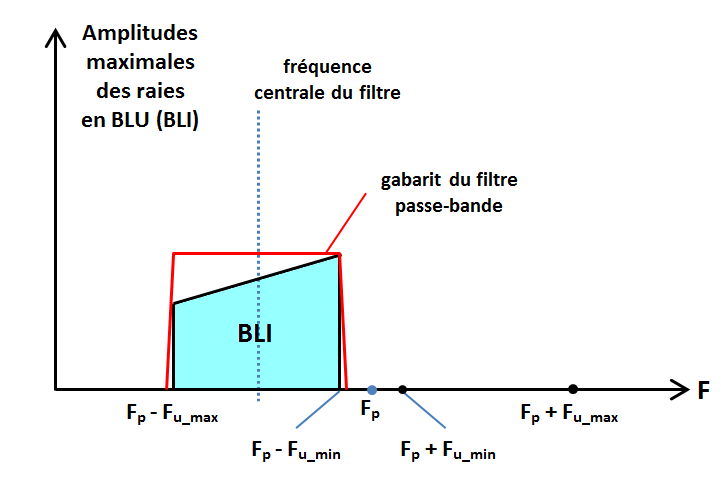
Expression du signal SBLU obtenu à la sortie du modulateur
Reprenons l'expression du signal SDBSP présent à la sortie d'un modulateur Double Bande latérale Sans Porteuse :
![\[ \boldsymbol{{{S}_{{DBSP}}}=\frac{{mE}}{2}\cos \left[ {({{\omega }_{p}}-{{\omega }_{u}})t} \right]+\frac{{mE}}{2}\cos \left[ {({{\omega }_{p}}+{{\omega }_{u}})t} \right]} \]](http://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-de1548b07ea0c9629b8b06903bb06fcd_l3.png "Rendered by QuickLaTeX.com")
- le premier terme représente la BLI, même s'il n'y a qu'une seule fréquence dans cette bande (pour le spectre : une seule raie),
- le second terme représente la BLS, même si, également, il n'y a qu'une seule fréquence dans cette bande (pour le spectre : à nouveau une seule raie). En ajoutant le filtre passe-bande décrit précédemment à la sortie du modulateur DBSP, l'un de ces deux termes disparaît en sortie du filtre.
En BLU BLS, l'expression du signal SBLU_BLS est donc la suivante :
(2) ![\begin{equation*} \boldsymbol{{{S}_{{BLU\_BLS}}}=\frac{{mE}}{2}\cos \left[ {\left( {{{\omega }_{p}}+{{\omega }_{u}}} \right)t} \right]=\frac{{mE}}{2}\cos \left[ {2\pi \left( {{{F}_{p}}+{{F}_{u}}} \right)t} \right]} \end{equation*}](http://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-5b8bd9e8e69e3e213909c72255e6d76c_l3.png "Rendered by QuickLaTeX.com")
(3) ![\begin{equation*} \boldsymbol{{{S}_{{BLU\_BLI}}}=\frac{{mE}}{2}\cos \left[ {\left( {{{\omega }_{p}}-{{\omega }_{u}}} \right)t} \right]=\frac{{mE}}{2}\cos \left[ {2\pi \left( {{{F}_{p}}-{{F}_{u}}} \right)t} \right]} \end{equation*}](http://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-9b129eafb7f69c7ef34826f7096eac1e_l3.png "Rendered by QuickLaTeX.com")
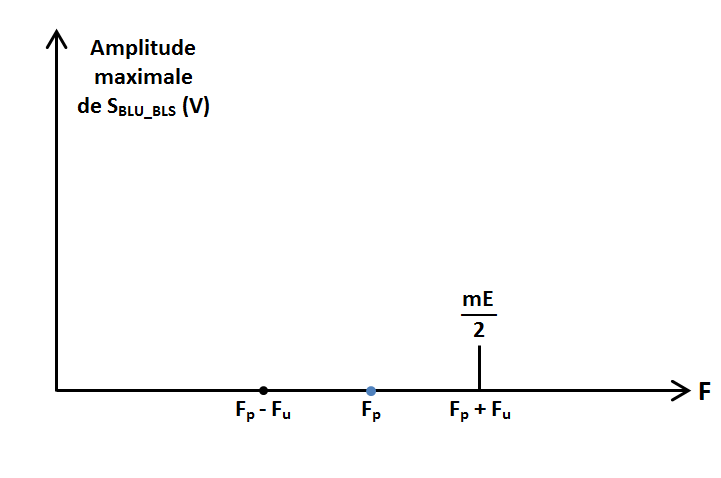
L'expression (2) est un simple cosinus affecté du coefficient mE/2. Les valeurs maximale et minimale de SBLU_BLS valent donc respectivement mE/2 et −mE/2. Le graphe est une simple sinusoïde de fréquence Fp + Fu :
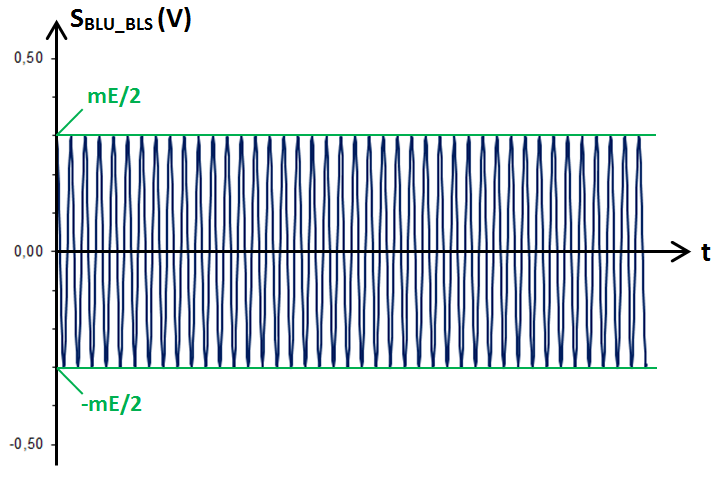
Graphes en BLU : la valeur de Fu a été modifiée par rapport à celle utilisée pour tracer les graphes dans les modes de modulation précédents (DBAP et DBSP). Graphe de SBLU_BLI en fonction du temps
L'expression (3) est aussi un simple cosinus affecté du coefficient mE/2. Les valeurs maximale et minimale de SBLU_BLI valent donc également respectivement mE/2 et −mE/2. Le graphe est une simple sinusoïde de fréquence Fp − Fu :
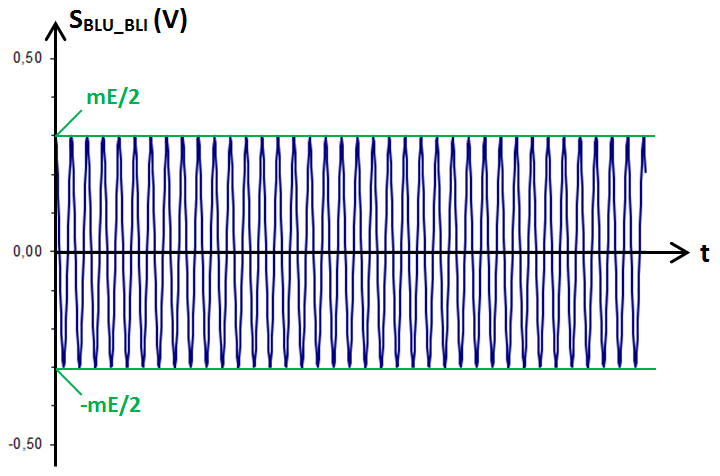
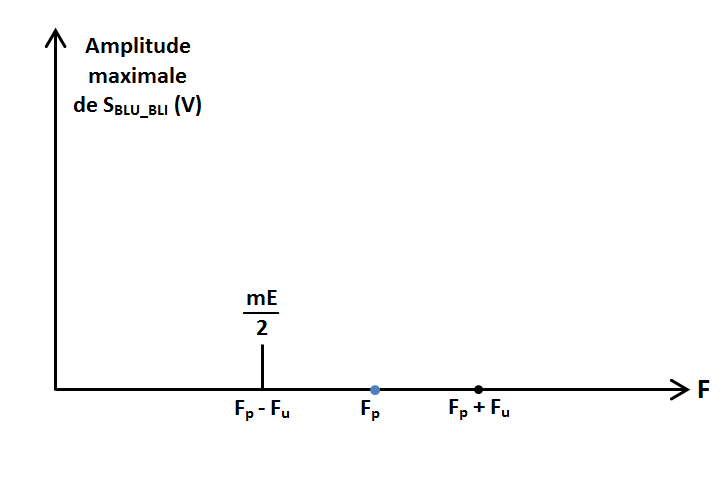
Les expressions (2) et (3) nous indiquent qu'un signal BLU peut toujours être ramené à une simple sinusoïde dont les valeurs maximale et minimale sont proportionnelles à m. Par conséquent, en BLU (sous-entendu « sans porteuse »), la surmodulation au sens que nous lui avions donné en modulation d'amplitude « classique » DBAP n'existe pas.
Néanmoins, dans un émetteur, ce signal BLU va être amplifié et/ou translaté en fréquence. Les dispositifs électroniques remplissant les fonctions correspondantes ne seront pas parfaitement linéaires : ils créeront de la distorsion qui viendra dégrader la pureté du signal émis.
Afin d'apprécier la linéarité de la chaîne d'émission, nous appliquerons à l'entrée BF du modulateur BLU le signal spécifique fourni par « un générateur 2 tons ». Nous reviendrons ultérieurement sur ce dispositif. << Causerie précédente Causerie suivante >> << Retour à la table des matières
