Radio-Club de Viry-Châtillon (91) - F5KEE

par F5FOD, Jean-Pierre Waymel

Valeur moyenne : définition
Quand un signal (tension ou courant) est périodique, il est parfois utile d'en définir puis d'en calculer la « valeur moyenne ». La définition de la valeur moyenne contient une intégrale. Nous allons donc l'exprimer plus simplement de la façon suivante :

   

Explication des termes de la définition
Dans cette causerie, tout ce qui sera dit au sujet d'une tension sera également applicable à un courant.
On commence par dessiner « la représentation graphique » de la tension u en fonction du temps, en prenant bien soin de repérer « u = 0 » (volt).
Puis, sur une durée égale à 1 période T, on calcule :
- l'aire Aire+ entre la courbe et l'horizontale u = 0 (volt) du côté des u positifs,
- l'aire Aire− entre la courbe et l'horizontale u = 0 (volt) du côté des u négatifs. La valeur moyenne de u notée est alors calculée de la façon suivante :

   

Autrement dit, on fait la somme des aires « sous » la courbe en affectant le signe − à l'aire située du côté des u négatifs et on divise le tout par la valeur de la période.

Exemples
Tension dite « rectangulaire »
Voici le graphe en fonction du temps d'une tension périodique u rectangulaire :

ABCDEFG représente 1 période de la tension u.
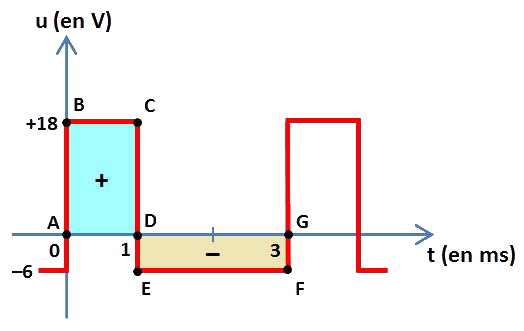
Cette période T est égale à 3 ms.
Nous allons maintenant calculer les aires « sous » la courbe pour 1 période de la tension. L'aire du rectangle ABCD représente l'aire entre la courbe et l'horizontale u = 0 (volt) du côté des u positifs. La longueur AB ou DC de ce rectangle est égale à 18 V et sa largeur AD ou BC est égale à 1 ms soit 0,001 s.
Par conséquent son aire vaut 18 × 0,001 = 0,018 Vs (volts×secondes). L'aire du rectangle DEFG représente l'aire entre la courbe et l'horizontale u = 0 (volt) du côté des u négatifs. La longueur DG ou EF de ce rectangle est égale à 2 ms soit 0,002 s et sa largeur DE ou GF est égale à 6 V.
Par conséquent son aire vaut 0,002 × 6 = 0,012 Vs.
Remarque : « longueur » et « largeur » sont considérées ici au sens strict d'une dimension du monde réel, elles sont donc toujours positives !
C'est pourquoi la largeur DE ou GF est égale à +6 V et non pas −6 V. Mais pour appliquer correctement la définition de la valeur moyenne à la partie négative de la tension, l'aire correspondante doit être affectée du signe −. La somme des aires sous la courbe est donc égale à 0,018 −0,012 = 0,006 Vs. Il ne nous reste plus qu'à diviser cette somme totale par la période T soit 3 ms c'est-à-dire 0,003 s :

   

Tension dite « en dent de scie »
Voici le graphe en fonction du temps d'une tension périodique u en dent de scie :

ABC représente 1 période de la tension u.
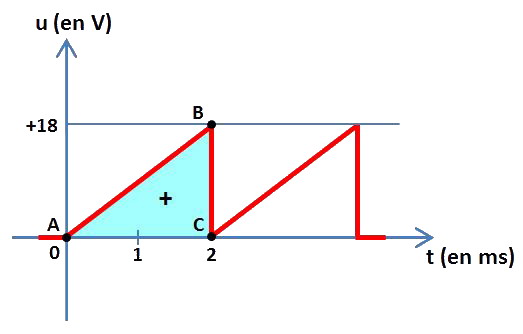
Cette période T est égale à 2 ms.
Nous allons maintenant calculer les aires « sous » la courbe pour 1 période de la tension. L'aire du triangle ABC représente l'aire entre la courbe et l'horizontale u = 0 (volt) du côté des  u positifs. La base AC de ce triangle est égale à 2 ms soit 0,002 s et sa hauteur CB est égale à 18 V.
Rappel : aire d'un triangle = (base × hauteur) / 2.
Par conséquent l'aire du triangle ABC vaut (0,002 × 18) / 2 = 0,018 Vs.
Il n'y a pas d'aire entre la courbe et l'horizontale u = 0 (volt) du côté des u négatifs. La somme des aires sous la courbe est donc égale à 0,018 Vs. Il ne nous reste plus qu'à diviser l'aire calculée par la période T soit 2 ms c'est-à-dire 0,002 s :

   

Tension dite « triangulaire »
Voici le graphe en fonction du temps d'une tension périodique u triangulaire :

ADEHI représente 1 période de la tension u.
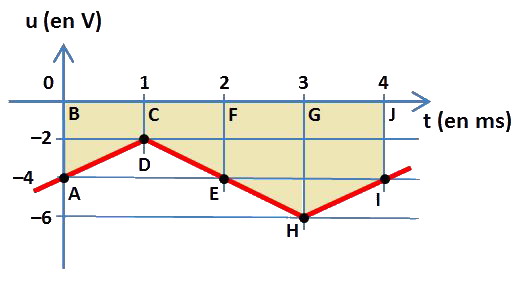
Cette période T est égale à 4 ms.
Nous allons maintenant calculer les aires « sous » la courbe pour 1 période de la tension. Il n'y a pas d'aire entre la courbe et l'horizontale u = 0 (volt) du côté des u positifs.
L'aire entre la courbe et l'horizontale u = 0 (volt) du côté des u négatifs est constituée :
- des aires des trapèzes ABCD et CDEF (ces aires sont égales),
- des aires des trapèzes EFGH et GHIJ (ces aires sont égales). Calculons l'aire du trapèze ABCD.
Rappel : aire d'un trapèze = demi-somme des bases × hauteur.
Ici AB et DC sont les bases et BC la hauteur.
D'où l'aire du trapèze ABCD = [(4 + 2) / 2] × 0,001 = 0,003 Vs.
Idem pour le trapèze CDEF. Calculons l'aire du trapèze EFGH.
Ici EF et HG sont les bases et FG la hauteur.
D'où l'aire du trapèze EFGH = [(4 + 6) / 2] × 0,001 = 0,005 Vs.
Idem pour le trapèze GHIJ. La somme des aires sous la courbe est donc égale à −(0,003 + 0,003 + 0,005 + 0,005) = −0,016 Vs. Il ne nous reste plus qu'à diviser cette somme des aires par la période T soit 4 ms c'est-à-dire 0,004 s :

   

Tension sinusoïdale
Voici le graphe en fonction du temps d'une tension périodique u sinusoïdale :

ABCDE représente 1 période T de la tension u.
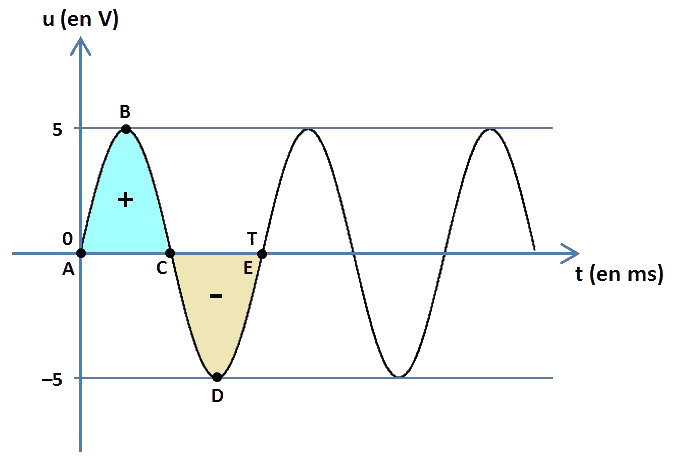
Cette fois-ci, il n'est pas possible de calculer géométriquement les aires « sous » la courbe ! Mais nous savons que l'alternance négative CDE est identique à l'alternance positive ABC au signe près de la tension. L'aire entre la courbe et l'horizontale u = 0 (volt) du côté des u négatifs est donc égale à l'aire entre la courbe et l'horizontale u = 0 (volt) du côté des u positifs mais elle devra être affectée du signe −.
Par conséquent, la somme des aires sous la courbe est nulle donc la valeur moyenne est nulle, ceci quelle que soit la valeur de T.

Propriété importante
Quand, sur 1 période, l'aire entre la courbe et l'horizontale u = 0 (volt) du côté des u positifs est égale à l'aire entre la courbe et l'horizontale u = 0 (volt) du côté des u négatifs, la valeur moyenne est nulle.

Et la valeur moyenne d'une tension continue ?
Voici le graphe en fonction du temps d'une tension u continue :

La valeur de la période est ici indéterminée puisque que le signal se reproduit identiquement à lui-même… à tout moment !
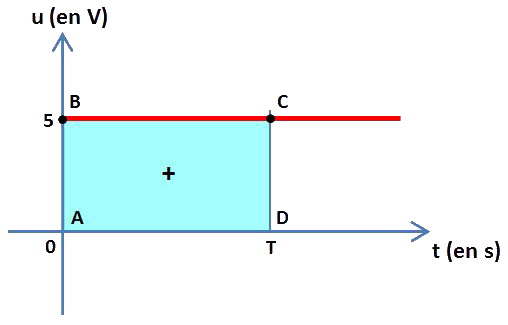
Appelons donc simplement cette période « T », sans en donner la valeur.
BC représente 1 période de la tension u.
Nous allons maintenant calculer les aires « sous » la courbe pour 1 période de la tension. Il n'y a pas d'aire entre la courbe et l'horizontale u = 0 (volt) du côté des u négatifs.
L'aire du rectangle ABCD représente l'aire entre la courbe et l'horizontale u = 0 (volt) du côté des u positifs. La longueur BC ou AD de ce rectangle est égale à T secondes et sa largeur AB ou DC est égale à 5 V.
Par conséquent son aire vaut T × 5 = 5T Vs. La somme des aires sous la courbe est donc égale à 5T Vs. Il ne nous reste plus qu'à diviser cette somme totale par la période T :

   

Bien entendu, si la tension continue a une valeur négative, on obtient cette valeur négative comme valeur moyenne.
Autrement dit : la valeur moyenne d'une tension continue est égale à cette tension continue.

 << Causerie précédente Causerie suivante >>  << Retour à la table des matières