Radio-Club de Viry-Châtillon (91) - F5KEE

par F5FOD, Jean-Pierre Waymel

Retour sur la tension triangulaire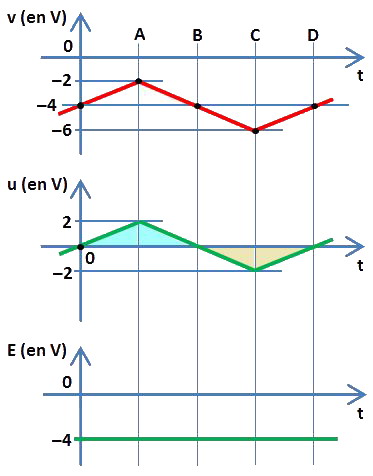

Sur le graphe du haut, nous retrouvons, en rouge, la tension triangulaire qui nous avait servi d'exemple pour calculer une valeur moyenne.
Cette fois-ci, appelons-la v.
Elle est périodique et son amplitude évolue entre −6 et −2 V. Les deux graphes en dessous, en vert, représentent :
- une tension triangulaire u, de même période mais évoluant entre −2 et +2 V, délivrée par un générateur de tension triangulaire G,
- une tension continue E, donc constante dans le temps, égale à −4 V, délivrée par un générateur de tension CC.
Connectons en série ces deux générateurs : nous obtenons la tension v !
En effet, il est facile de vérifier au moyen des trois graphes que les tensions E, u et v obéissent à la relation suivante :

   

Par exemple, au temps « A » :
E = −4 V
u = +2 V
v = −4 + 2 = −2 V ou au temps « B » :
E = −4 V
u = 0 V
v = −4 + 0 = −4 V ou à n'importe quelle valeur du temps t. Autrement dit, il est toujours possible de considérer qu'une tension donnée est la somme de deux ou plusieurs autres tensions.

Valeur moyenne d'une somme de deux tensions ayant la même période
Prenons deux tensions périodiques a et b ayant la même période.
Et appelons v leur somme :

   

On démontre que la valeur moyenne de v (notée ) est égale à la somme de la valeur moyenne de a (notée ) et de la valeur moyenne de b (notée ). Ce qui peut s'écrire ainsi :

   

Appliquons cette relation à notre tension triangulaire
La tension E ayant une période indéterminée, nous pouvons lui attribuer celle de u.
La valeur moyenne de E est égale à E.
La valeur moyenne de u est égale à 0 car l'aire entre la courbe et l'horizontale u = 0 (volt) du côté des u positifs est égale à l'aire entre la courbe et l'horizontale u = 0 (volt) du côté des u négatifs. Comme les tensions E et u ont la même période et que v = E + u, nous pouvons calculer la valeur moyenne de v de la façon suivante :

   

La valeur moyenne de v est donc tout simplement égale à E, soit −4 V.
La méthode des aires « sous la courbe » donnait le même résultat (ouf !) mais il avait fallu calculer des aires de trapèzes…

Un autre exemple de calcul de valeur moyenne utilisant la somme de deux tensions ayant la même période

Sur le graphe du haut, en rouge, nous observons une tension v qui ressemble à une tension sinusoïdale mais qui n'évolue pas autour de 0 V.
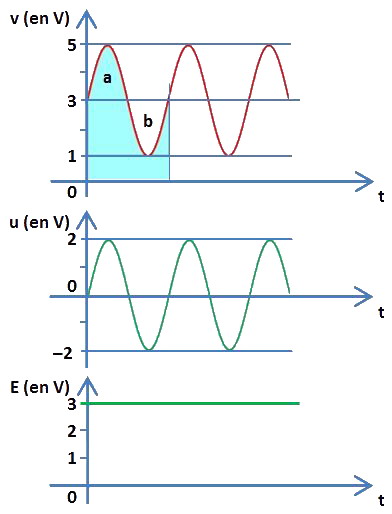
Nous pouvons considérer que v est la somme des tensions E et u, représentées par les graphes en vert :

   

Donc à nouveau :

   

E étant égal à 3 V, la valeur moyenne de v est égale à 3 V.
La tension v est une sinusoïde qui évolue autour de +3 V, entre +5 et +1 V. La méthode de calcul des aires pourrait paraître ici compliquée. Mais une astuce permet de trouver rapidement le résultat. L'aire à calculer est celle qui est colorée sous le graphe de v.
Retirons de cette aire à calculer l'aire a située entre la ligne horizontale 3 V et l'alternance qui se situe au-dessus de cette ligne. Reportons cette aire dans l'aire b située entre la ligne horizontale 3 V et l'alternance qui se situe en dessous. Nous n'avons rien changé à l'aire totale à calculer si ce n'est qu'elle est devenue maintenant celle d'un rectangle !
L'aire de ce rectangle vaut 3 × T, T étant la période de v.
La valeur moyenne de v étant cette aire divisée par T, nous retrouvons bien nos 3 V (3 × T / T = 3).

Composante continue : définition
La valeur moyenne d'une tension périodique est également appelée « composante continue ». Les deux exemples précédents illustrent bien ce nouveau terme : la tension v évolue « de part et d'autre » d'une tension continue E qui est donc sa « composante continue ».

 << Causerie précédente Causerie suivante >>  << Retour à la table des matières