par F5FOD, Jean-Pierre Waymel
Qu'est-ce que l'énergie ?Selon Wikipedia :
L’énergie est un concept relié à ceux d'action, de force et de durée : la mise en œuvre d'une action nécessite de maintenir une certaine force pendant une durée suffisante pour vaincre les inerties et résistances qui s'opposent à ce changement. L'énergie qui aura été nécessaire pour accomplir finalement l'action envisagée rend compte à la fois de la force et de la durée pendant laquelle elle aura été exercée.
L'inertie : en simplifiant, l'inertie d'un corps est sa tendance à conserver sa vitesse ; en l'absence d'influence extérieure, tout corps ponctuel perdure dans un mouvement rectiligne uniforme. Si cette vitesse était nulle, elle reste nulle. Quelles sont les différentes formes de l'énergie ?
Empruntons le tableau suivant à l'excellent site de Carol Eicher et André Mousset, science.lu :
| Porteur d'énergie | Forme d'énergie |
| Corps en mouvement (voiture en mouvement, vent) | Énergie cinétique |
| Corps situé à une certaine altitude (eau retenue par un barrage) | Énergie potentielle de pesanteur |
| Corps élastique déformé (ressort comprimé) | Énergie (potentielle) élastique |
| Corps chargé électriquement (nuage orageux) | Énergie électrique |
| Corps chaud (radiateur, flamme) | Énergie calorifique (ou énergie thermique) |
| Pile/accumulateur électrique | Énergie chimique |
| Onde électromagnétique (rayonnement solaire, micro-ondes) | Énergie rayonnante |
| Noyau d'uranium, noyau d'hydrogène | Énergie nucléaire |
| Tout corps de masse m | Énergie de masse, d'après Albert Einstein : E = mc2, c étant la vitesse de la lumière |
Soit une résistance R connectée à une source de tension continue U et parcourue par un courant continu I.
L'énergie électrique fournie par cette source pendant un temps t se transforme dans la résistance en énergie thermique E (loi de Joule) de la façon suivante :
(1) ![]()
U = 12 V
I = 2 A
t = 1 h soit 3600 s
E = 12 × 2 × 3600 = 86400 J = 86,4 kJ. Appliquons maintenant la loi d'Ohm à notre résistance R :
![]()
![]()
![]()
![]()
(2) ![]()
Soit un réfrigérateur à monter au premier étage d'un immeuble.
Supposons que l'énergie nécessaire pour effectuer cette action soit égale à 1300 J.
Le moteur de l'ascenseur sera d'autant plus « puissant » qu'il pourra effectuer rapidement l'opération.
S'il le fait en 10 secondes, on dira que ce moteur a une puissance égale à 1300/10 = 130 watts.
S'il le fait en 5 secondes, on dira que ce moteur a une puissance égale à 1300/5 = 260 watts. En effet, la puissance P est égale à l'énergie E divisée par le temps t :
![]()
![]()
Pour calculer la puissance P, il suffit simplement de diviser l'énergie exprimée dans l'expression (2) par le temps t, ce qui donne :
![]()
La structure physique de la résistance doit permettre la dissipation de la chaleur correspondante. Sinon le composant sera abîmé voire carrément détruit ! Et la puissance en courant non continu ?
Nous ne considèrerons que le cas des signaux périodiques (tensions et courants). Prenons momentanément l'exemple d'une source de tension alternative sinusoïdale délivrant la tension u suivante :
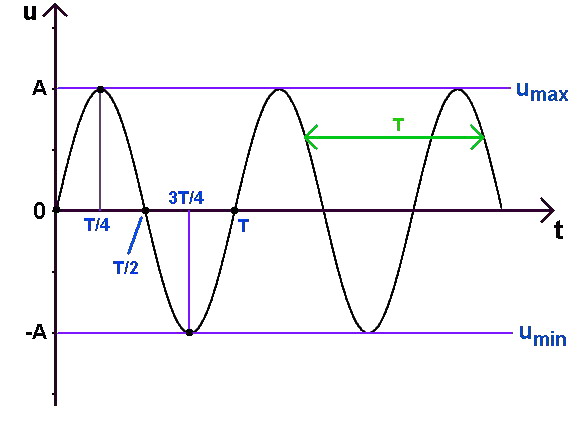
Pendant l'alternance négative, la tension change de signe et le courant change de sens par rapport à ce qu'ils étaient pendant l'alternance positive.
Est-ce à dire que l'effet thermique constatée dans la résistance sera différent d'une alternance à l'autre ?
La réponse est « non » : la résistance ne va pas refroidir pendant l'alternance négative… Elle chauffera exactement de la même manière qu'elle a chauffé pendant l'alternance positive. Le souci est plutôt qu'au sein d'une période T, la tension u est différente à chaque instant : u est la valeur instantanée de la tension.
De même pour le courant i.
D'ailleurs ils sont liés par la loi d'Ohm « instantanée » :
![]()
Le concept de « valeur efficace » a alors été créé : la valeur efficace d'une tension périodique est la valeur qu'aurait une tension continue produisant les mêmes effets physiques, par exemple la même élévation de température, dans les mêmes conditions.
Cette valeur efficace se calcule mathématiquement : on élève la tension au carré, on calcule la valeur moyenne du résultat et enfin on effectue la racine carrée de cette valeur moyenne. D'où le terme anglais : « RMS », « Root Mean Square ». « Square » (« carré ») : l'élévation au carré, « Mean » (« moyen ») : la valeur moyenne du carré et « Root » (« racine ») : la racine carrée de la valeur moyenne !
Idem pour le courant.
On parle donc de volts et d'ampères efficaces ou de volts et ampères RMS. Pour la tension alternative sinusoïdale prise comme exemple, on démontre que les valeurs efficaces et maximales des tensions et courants sont liées par les formules suivantes :
(3) ![]()
(4) ![]()
![]()
![]()
La valeur « 230 V » est une valeur efficace.
On en déduit la valeur maximale, appelée aussi valeur crête :
1. Pour tout autre signal périodique non sinusoïdal, les formules ci-dessus où apparaît
2. La valeur efficace d'une somme de deux tensions périodiques n'est pas égale à la somme de leurs valeurs efficaces. Connectons maintenant notre résistance R à une source de tension périodique de forme quelconque.
On démontre que la puissance P se calcule de la façon suivante :
![]()
![]()
![]()
![]()
![]()
![]()
Or, par définition,
Donc :
![]()
![]()
![]()