par F5FOD, Jean-Pierre Waymel
Le courant sinusoïdal iDans cette causerie, chaque composant sera considéré comme parfait.
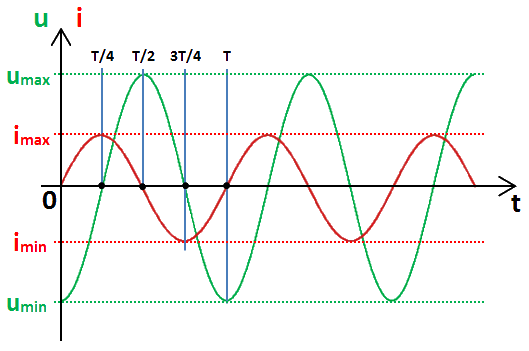
Il sera traversé par un courant sinusoïdal i dont voici la forme :
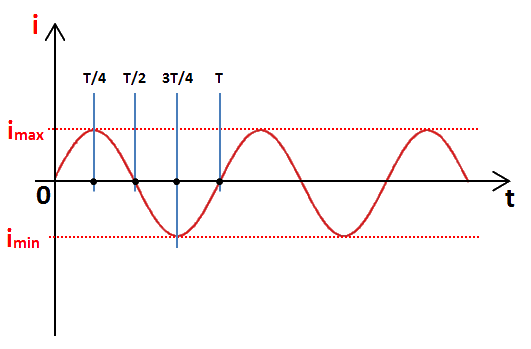
- période : T,
- fréquence : F = 1/T,
- pulsation : ω = 2πF = 2π/T,
- passages par 0 (ampère) à t = 0, t = T/2 et t = T,
- passage au maximum imax à t = T/4,
- passage au minimum imin = −imax à t = 3T/4. Le courant sinusoïdal i traverse une résistance R de résistance R
Un peu de vocabulaire
Le composant « résistance » devrait être appelé « résistor », le mot « résistance » exprimant la propriété physique du composant.
Mais en France, la plupart du temps, le terme « résistance » et son abréviation « R » sont utilisés pour désigner à la fois le composant, sa propriété et sa valeur (en ohms). La tension u aux bornes de la résistance R
Aux bornes de la résistance R traversée par notre courant i, nous obtenons une tension u :
- sinusoïdale,
- en phase avec le courant i.
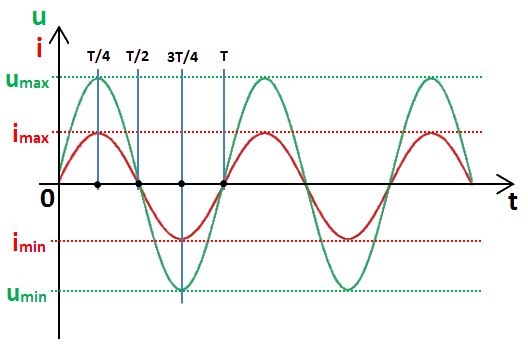
- la même période : T,
- la même fréquence : F = 1/T,
- la même pulsation : ω = 2πF = 2π/T. Les valeurs maximales de u et de i obéissent à la relation suivante :
(1) ![]()
À partir d'un point A, traçons une ligne horizontale vers la droite.
Sur cette ligne, traçons une flèche partant également du point A et se dirigeant également vers la droite.
La longueur de cette flèche sera proportionnelle à la valeur maximale du courant i, soit imax.
Bien entendu, au préalable, une échelle de courant aura été déterminée, par exemple 1 cm pour 1 mA.
C'est la flèche rouge sur le diagramme suivant :
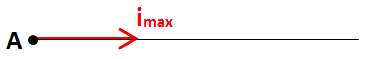
La longueur de cette seconde flèche sera proportionnelle à la valeur maximale de la tension u, soit umax.
Bien entendu, au préalable, une échelle de tension aura été déterminée, par exemple 1 cm pour 10 V. L'angle en A entre la flèche de la tension u et la flèche du courant i sera égal à l'angle de déphasage de u par rapport à i.
Ici, dans le cas de la résistance (parfaite), i et u sont en phase. L'angle de déphasage est donc égal à 0°.
Par conséquent, la flèche de la tension se trouvera « sur » la flèche du courant.
Dans la représentation ci-après, nous avons décalé verticalement la flèche (verte) de la tension afin de pouvoir la visualiser entièrement :

Un vecteur est défini par une direction, un sens et une longueur.
Par exemple, pour le vecteur « courant i » :
- sa direction est « l'horizontale »,
- son sens est « vers la droite »,
- sa longueur est ici égale à imax. Le courant sinusoïdal i traverse une bobine L d'inductance L
Un peu de vocabulaire
Le composant « bobine » est parfois appelé « bobinage », ce qui est encore correct bien que le terme « bobinage » exprime plutôt l'opération permettant de réaliser… une bobine !
Par contre, les mots « inductance » et « self » sont impropres à désigner une bobine car ils désignent la propriété physique du composant.
Néanmoins, l'abréviation « L » est utilisée pour désigner à la fois le composant, sa propriété et sa valeur (en henrys) ! La tension u aux bornes de la bobine L
Aux bornes de la bobine L traversée par notre courant i, nous obtenons une tension u :
- sinusoïdale,
- en quadrature avance sur le courant i.
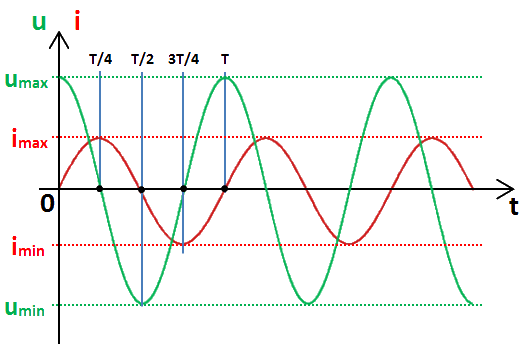
- la même période : T,
- la même fréquence : F = 1/T,
- la même pulsation : ω = 2πF = 2π/T. La tension u est en avance d'un quart de période (T/4) sur le courant i.
L'angle de déphasage de u par rapport à i est égal à +90°. Les valeurs maximales de u et de i obéissent à la relation suivante :
(2) ![]()
Traçons la flèche imax comme nous l'avons fait pour la résistance R :
L'angle en A entre la flèche de la tension u et la flèche du courant i sera égal à l'angle de déphasage de u par rapport à i, soit +90° pour notre bobine (parfaite).
Par conséquent, la flèche de la tension u sera perpendiculaire à la flèche du courant i et orientée vers le haut car l'angle est positif (ce qui correspond au sens « trigonométrique », c-à-d contraire au sens des aiguilles d'une montre) :
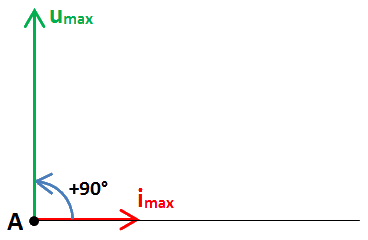
Un peu de vocabulaire
Le composant « condensateur » est parfois appelé « capacité » ou « capa », ce qui est incorrect car ces termes désignent la propriété physique du composant.
Néanmoins, l'abréviation « C » est utilisée pour désigner à la fois le composant, sa propriété et sa valeur (en farads) ! La tension u aux bornes du condensateur C
Aux bornes du condensateur C traversé par notre courant i, nous obtenons une tension u :
- sinusoïdale,
- en quadrature retard sur le courant i.
- la même période : T,
- la même fréquence : F = 1/T,
- la même pulsation : ω = 2πF = 2π/T. La tension u est en retard d'un quart de période (T/4) sur le courant i.
L'angle de déphasage de u par rapport à i est égal à −90°. Les valeurs maximales de u et de i obéissent à la relation suivante :
(3) ![]()
Traçons la flèche imax comme nous l'avons fait pour la résistance R :
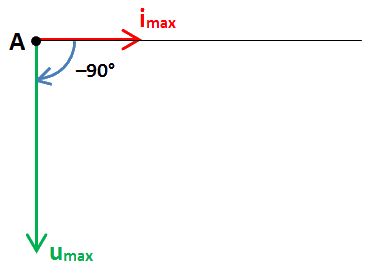
L'angle en A entre la flèche de la tension u et la flèche du courant i sera égal à l'angle de déphasage de u par rapport à i, soit −90° pour notre condensateur (parfait).
Par conséquent, la flèche de la tension u sera perpendiculaire à la flèche du courant i et orientée vers le bas car l'angle est négatif (ce qui correspond au sens contraire du sens « trigonométrique », c-à-d dans le sens des aiguilles d'une montre) :
Réactance
Quand la tension u aux bornes d'un composant est en quadrature avec le courant i qui le traverse, on appelle « réactance X » le rapport suivant :
![]()
C'est la réactance XL d'une bobine.
La pulsation ω étant égale à 2πF, nous obtenons :
![]()
C'est la réactance XC d'un condensateur :
![]()
La tension u et le courant i étant sinusoïdaux, nous pouvons également utiliser leurs valeurs efficaces :
![]()
![]()
![]()
