Formation à l’examen : bobine
par F5FOD, Jean-Pierre Waymel
Rappel de vocabulaireEnroulons un fil conducteur : nous fabriquons une « bobine », un « solénoïde », un « bobinage ».
« Inductance » ou « self » sont des noms impropres pour dénommer le composant « bobine » car ils désignent en réalité sa propriété électromagnétique. Néanmoins la même lettre L est quasiment toujours utilisée pour repérer une bobine sur un schéma et/ou pour donner la valeur de son inductance… Un seul tour fournissant une seule spire est déjà une bobine. Et comme nous le verrons plus tard, même non enroulé, un fil conducteur est aussi une bobine ! Quelques exemples de bobines
Un solénoïde peut être bobiné « sur l'air » :
L'ancien symbole est celui de gauche, le symbole actuel celui de droite :
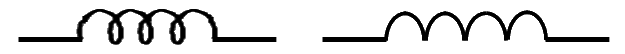
Pour une bobine L donnée, appelons :
n son nombre de spires,
S la surface d'une spire,
long la longueur totale bobinée. Voici une formule donnant de façon tout à fait théorique la valeur de l'inductance L de cette bobine L, inductance exprimée en henrys (H) :
(1) 
![\[ \boldsymbol{C={{\varepsilon }_{0}}{{\varepsilon }_{r}}\frac{S}{{e}}} \]](https://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-993ece99a9a72a037cf298513ec63c4e_l3.png "Rendered by QuickLaTeX.com")
Finalement, ce qui est important à retenir − et qui est au programme de l'examen − se résume ainsi :
- l'inductance d'une bobine est proportionnelle au carré du nombre de ses spires,
- l'inductance d'une bobine est proportionnelle à la surface d'une spire (ou au carré de son rayon ou au carré de son diamètre),
- l'inductance d'une bobine est inversement proportionnelle à sa longueur bobinée,
- l'inductance d'une bobine est proportionnelle à la perméabilité relative μr de son noyau, cf. ci-après. La perméabilité μ
La perméabilité μ, exprimée en henrys par mètre (H/m), est ainsi définie :
![\[ \boxed{\boldsymbol{\mu ={{\mu }_{0}}{{\mu }_{r}}}} \]](https://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-24af67e6597293d4167267890d7a3a6c_l3.png "Rendered by QuickLaTeX.com")
![\[ \boldsymbol{{{\mu }_{0}}=4\pi {{10}^{{-7}}} \textbf{ H/m}} \]](https://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-ef39801b86573fb18250e21d77d2843e_l3.png "Rendered by QuickLaTeX.com")
![\[ \boldsymbol{{{\varepsilon }_{0}}\mu {}_{0}{{c}^{2}}=1} \]](https://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-a0e08655ee594e3ca73aeb21abea08b4_l3.png "Rendered by QuickLaTeX.com")
Quand la bobine est bobinée « sur l'air », le matériau présent au sein des spires est… de l'air ! Quand elle est bobinée sur un mandrin, ce dernier peut être muni d'un « noyau ». C'est alors le matériau constituant ce noyau qu'il faut considérer. De même si le bobinage est effectué sur un tore.
Sur un schéma, la présence d'un noyau se traduit en général par plusieurs traits pleins ou pointillés dessinés parallèlement au symbole de la bobine. On distingue :
- les matériaux diamagnétiques, comme l'argent, le cuivre, le plomb, le zinc, etc. qui s'aimantent dans le sens contraire du champ magnétique, avec μr ≤ 1,
- les matériaux paramagnétiques, comme l'air, l'aluminium, le platine, etc. qui s'aimantent dans le sens du champ magnétique, avec μr ≥ 1,
- les matériaux ferromagnétiques, comme le cobalt, le fer, le mu-métal, le nickel, etc., avec μr >> 1. À noter cependant que beaucoup de matériaux diamagnétiques et paramagnétiques ont une perméabilité relative très proche de 1 :
- air (sec) : μr = 1,
- cuivre : μr = 1 − 10-5 = 0,99999,
- argent : 1 − 2,6 × 10-5 = 0,999974. Voici quelques exemples de matériaux ferromagnétiques :
- le cobalt : μr = 250,
- le nickel : μr = 600,
- les ferrites : μr = 20 à 15000,
- le fer : μr = 5000,
- le mu-métal : μr = 100000. La valeur de la perméabilité relative des matériaux ferromagnétiques dépend de l'excitation magnétique, de la température et de la fréquence de travail… En pratique
Seuls les effets « qualitatifs » des formules de calcul d'inductance sont au programme de l'examen. C'est l'objet de ce paragraphe.
Soit une bobine « à air » (μr = 1) ayant une inductance L égale à 25 µH.
Si on triple son nombre de spires, son inductance sera multiplié par 32 :
L = 25 × 9 = 225 µH.
Si on divise par 2 le diamètre des spires (leur surface sera divisée par 4), son inductance sera divisée par 4 :
L = 25 / 4 = 6,25 µH.
Si on augmente de 5 % la longueur bobinée, son inductance sera divisée par 1,05 :
L = 25 / 1,05 = 23,8 µH environ.
Si on introduit dans la bobine un noyau de ferrite ayant une perméabilité relative égale à 300, son inductance sera multipliée par 300 :
L = 25 × 300 = 7500 µH. Formule de Nagaoka
Pour info uniquement.
La formule de Nagaoka s'applique à des bobines composée d'une seule couche de spires jointives et dont le rapport longueur sur diamètre est supérieur ou égal à 0,4. Mais ce nombre lui-même est sujet à variations dans la littérature. En réalité, il ne s'agit pas d'une formule mais d'un tableau de calcul. Voici néanmoins… l'une des formules souvent utilisée (il y en a d'autres !) :
(2) 
d = diamètre d'une spire en mm,
long = longueur du bobinage en mm.
Attention : ici, L est exprimée en µH. Dans la formule (1), remplaçons μ0 par sa valeur, exprimons le diamètre et la longueur en mm, l'inductance en µH et arrondissons π2 à 10. Nous obtenons :
![\[ \boldsymbol{L={{\mu }_{r}}{{n}^{2}}\frac{{{{d}^{2}}}}{{1000long}}} \]](https://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-e38322c664a4845797143de6b959b3f5_l3.png "Rendered by QuickLaTeX.com")
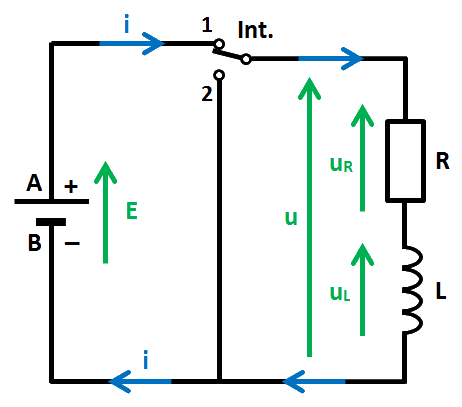
La pile, de force électromotrice égale à E, est parfaite : sa résistance interne est donc nulle.
Comme exemple, nous prendrons E = 10 V, R = 1 kΩ et L = 10 mH.
La bobine est considérée comme parfaite (aucunes pertes) et n'a pas été mise en circuit auparavant. Le quotient L / R va jouer un rôle fondamental.
Il est appelé « constante de temps » et désigné par la lettre grecque τ (tau) :
![\[ \boldsymbol{\tau =\frac{L}{R}}} \]](https://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-1c74b438ebf667f43c8f6a9d0c37c554_l3.png "Rendered by QuickLaTeX.com")
Si R est exprimée en ohms et L en henrys, τ sera en secondes.
Dans notre exemple : τ = 10 × 10-3 / 10-3 = 0,000010 s = 10 µs. Maintenant basculons l'interrupteur « Int. » en position 1.
Voici la courbe donnant la valeur du courant i, traversant la résistance R et la bobine L, en fonction du temps :
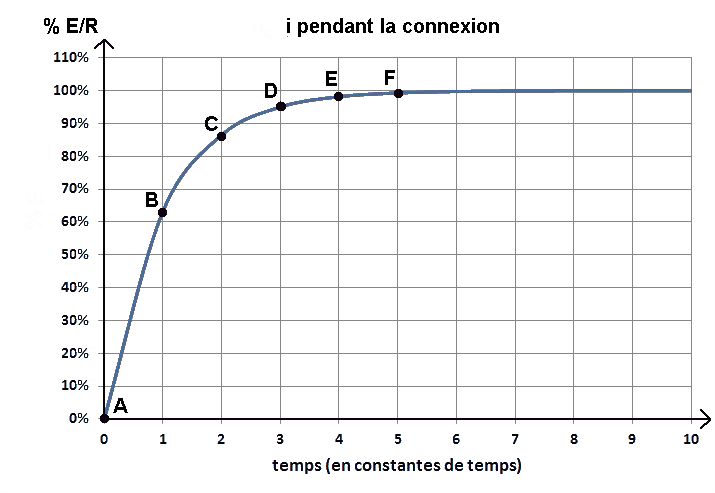
Dans notre exemple, « 3 » représente donc 3 × 10 = 30 µs.
L'axe vertical est l'axe du courant i traversant la résistance R et la bobine L, en pourcentage de sa valeur maximale E / R. Ici E / R = 10 mA. Dans notre exemple, « 40 % » représente donc 0,40 × 10 = 4 mA. La valeur maximale E / R correspond à la valeur qu'aurait le courant i si on remplaçait la bobine L par un court-circuit. Dans les quatre alinéas suivants, « en A », « en B », « en C », « en D », « en E » et « en F » feront référence aux points correspondants sur la courbe. En A, nous basculons l'interrupteur « Int. » en position 1 : ce sera « le temps 0 ».
Le courant i est nul au départ. Ce courant i augmente ensuite « rapidement ».
En B, au bout d'une constante de temps (10 µs), il vaut déjà 63 % de E / R (6,3 mA). Puis il augmente encore, mais moins rapidement.
En C, au bout de deux constantes de temps (20 µs), il vaut 86 % de E / R (8,6 mA). Et enfin, il augmente de plus en plus lentement.
En D, au bout de trois constantes de temps (30 µs), il vaut 95 % de E / R (9,5 mA).
En E, au bout de quatre constantes de temps (40 µs), il vaut 98 % de E / R (9,8 mA).
En F, au bout de cinq constantes de temps (50 µs), il vaut 99 % de E / R (9,9 mA). Il n'atteindra jamais les 100 %, si ce n'est… au bout d'un temps infini !
Quant à la tension uL, partie de E, elle va diminuer en suivant un régime identique pour atteindre une valeur quasiment nulle. La bobine se comporte alors comme un court-circuit : un courant pratiquement maximal la traverse et la tension à ses bornes est pratiquement nulle… Les équations du courant et de la tension en fonction du temps contiennent des « exponentielles » mais il n'est pas nécessaire de les détailler ici car le développement correspondant ne fait pas partie du programme de l'examen. Lors de la connexion d'une bobine à une source de tension continue, il suffira de mémoriser :
a) au bout d'1 seule constante de temps, le courant qui la traverse atteindra déjà 63 % du résultat final soit environ les 2/3,
b) au bout de 5 constantes de temps, ce courant atteindra 99 % du résultat final. Effet du circuit RL pendant la connexion à une source de tension continue
La bobine s'oppose à l'établissement du courant dans le circuit : plus exactement, elle le retarde. Au début de la connexion, elle peut être assimilée à un circuit ouvert : courant nul et tension de la source à ses bornes.
Puis le courant augmente et la tension aux bornes de la bobine diminue. Lors de la connexion d'une bobine à une source de tension continue, en comparant le fonctionnement du circuit correspondant à celui de la charge en tension d'un condensateur avec une constante de temps égale à RC, on pourrait écrire que nous avons ici la « charge en intensité » d'une bobine avec une constante de temps égale à L / R. Déconnexion d'une source de tension continue via une résistance
Basculons maintenant l'interrupteur « Int. » en position 2 :
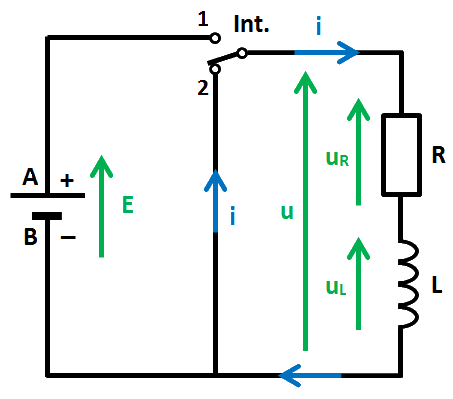
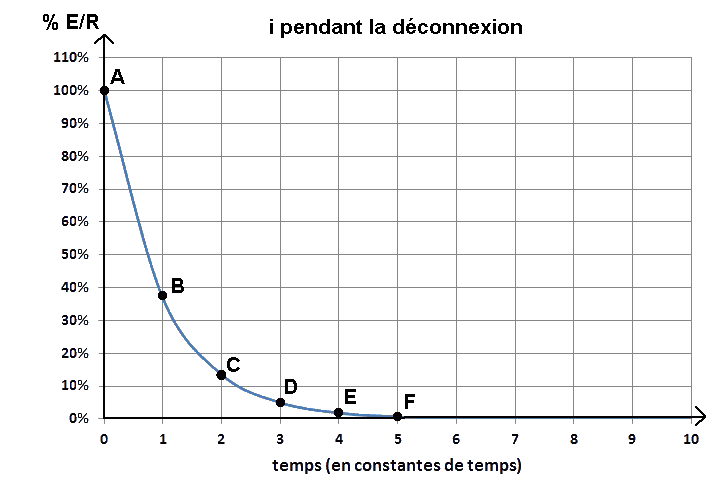
À ce temps 0, le courant i est pratiquement égal à E / R, d'où le 100 %. Ce courant décroît ensuite « rapidement ».
En B, au bout d'une constante de temps (10 µs), il ne vaut plus que 37 % de E / R (3,7 mA).
Remarquons que 37 %, c'est 100 % − 63 %. Puis il décroît encore, mais moins rapidement.
En C, au bout de deux constantes de temps (20 µs), il vaut 14 % de E / R (1,4 mA).
Remarquons que 14 %, c'est 100 % − 86 %. Et enfin, il décroît de plus en plus lentement.
En D, au bout de trois constantes de temps (30 µs), il vaut 5 % de E / R (0,5 mA), soit 100 % − 95 %.
En E, au bout de quatre constantes de temps (40 µs), il vaut 2 % de E / R (0,2 mA), soit 100 % − 98 %.
En F, au bout de cinq constantes de temps (50 µs), il vaut 1 % de E / R (0,1 mA), soit 100 % − 99 %. Il n'atteindra jamais le 0 %, si ce n'est… au bout d'un temps infini ! Les courbes du courant pendant la connexion et pendant la déconnexion d'un circuit RL donné sont symétriques par rapport à la ligne horizontale « 50 % de E / R ». Lors de la déconnexion d'une bobine d'une source de tension continue, il suffira de mémoriser :
a) au bout d'1 seule constante de temps, le courant qui la traverse aura déjà perdu 63 % de sa valeur initiale soit environ les 2/3,
b) au bout de 5 constantes de temps, ce courant aura perdu 99 % de sa valeur initiale. Effet du circuit RL pendant la déconnexion d'une source de tension continue
La bobine s'oppose à la disparition du courant dans le circuit : plus exactement, elle la retarde. Lors de la déconnexion d'une bobine d'une source de tension continue, en comparant le fonctionnement du circuit correspondant à celui de la décharge en tension d'un condensateur avec une constante de temps égale à RC, on pourrait écrire que nous avons ici la « décharge en intensité » d'une bobine avec une constante de temps égale à L / R. Les pertes dans une bobine
En CC (Courant Continu)
Les pertes se résument aux pertes par effet Joule dans le cuivre des spires. En CA (Courant Alternatif)
Pertes dans le fil constituant la bobine
Il s'agit également de pertes par effet Joule. Cependant, il faut tenir tenir compte de « l'effet de peau » : le courant ne circule qu'en surface des conducteurs, jusqu'à une profondeur δ (delta) dépendant de la fréquence, ce qui en augmente la résistance donc les pertes !
Cette profondeur δ se calcule de la façon suivante :
![\[ \boldsymbol{\delta =\sqrt{{\frac{{2\rho }}{{\mu \omega }}}}} \]](https://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-0e8e7abed5f6215c5388bf3bb7a46859_l3.png "Rendered by QuickLaTeX.com")
ρ = résistivité du métal utilisé pour réaliser les spires,
μ = perméabilité de ce métal,
ω = pulsation de la fréquence de travail.
Prenons l'exemple du cuivre dont la résistivité est égale à 1,8 × 10-8 Ω.m :
- à 20 kHz, δ = 477 µm,
- à 1 MHz, δ = 68 µm,
- à 3,5 MHz, δ = 36 µm,
- à 28 MHz, δ = 13 µm,
- à 144 MHz, δ = 6 µm,
- à 432 MHz, δ = 3 µm,
- à 10 GHz, δ = 0,7 µm. C'est la raison pour laquelle, en VHF/UHF, on utilise parfois du cuivre argenté pour réaliser les bobines. En HF, on utilise du « fil de Litz ». Le fil est divisé en brins plus fins isolés électriquement les uns des autres. Chacun de ces brins doit avoir un diamètre inférieur à la valeur de l'épaisseur de peau δ à la fréquence de travail (pour du cuivre, à 1 MHz : diamètre inférieur à 0,07 mm).
Cependant, même lorsque le fil est composé de brins isolés électriquement, les effets de proximité entre les fils rendent le fil encore résistif à haute fréquence car le courant ne se répartit pas également entre tous les brins. Afin de lutter contre ces effets de proximité, il faut que chaque brin ne soit pas toujours situé au même endroit du fil mais alterne entre différentes positions. Ainsi le courant se répartit équitablement entre tous les brins. Pour ce faire, l'une des solutions consiste à tresser ou toronner les brins entre eux. Le nom de « Litz » n'est pas celui de l'inventeur du procédé ! Ce nom provient d'une abréviation du terme allemand « Litze » qui signifie « tresse ». On utilise aussi le terme « fil divisé ». Pertes dans le noyau, si la bobine en est munie
On retrouve ici les mêmes pertes que nous avions étudiées dans le circuit magnétique du transformateur :
- pertes par courants de Foucault : le flux magnétique induit des courants au sein du noyau qui s'échauffe alors par effet joule. Rappelons que les pertes par courants de Foucault sont proportionnelles au carré de la fréquence,
- pertes par hystérésis : les changements de direction du flux oblige le matériau du noyau à se réorienter. Ce qui ne se fait pas sans frottements, créant ainsi des pertes. Capacités parasites
Bien qu'il ne s'agisse pas de pertes à proprement parler, une bobine présente des capacités parasites. En effet, une paire de spires adjacentes peut être vue comme deux armatures d'un condensateur !
Le bobinage en nid(s) d'abeilles permet de réduire ces capacités parasites. La bobine en régime sinusoïdal
Rappels :
- le module de l'impédance d'une bobine est égal à Lω,
- la tension à ses bornes est en quadrature avance par rapport au courant qui la traverse. << Causerie précédente Causerie suivante >> << Retour à la table des matières
