Formation à l’examen : circuit RLC série, en régime sinusoïdal
par F5FOD, Jean-Pierre Waymel
AvertissementUne impédance Z s'exprime mathématiquement au moyen d'un nombre complexe contenant deux informations :
- son module |Z| : c'est la valeur de l'impédance, en ohms,
- son argument φ : c'est le déphasage de la tension par rapport au courant. Il s'agit donc d'un angle, en radians ou en degrés.
Par défaut, à partir de cette causerie, l'expression « module de l'impédance » sera remplacée par le seul terme « impédance », noté Z en abrégé. 1. Circuit RsLsCs série (indice « s » pour « série »)
Nous allons calculer l'impédance Zs du circuit suivant :
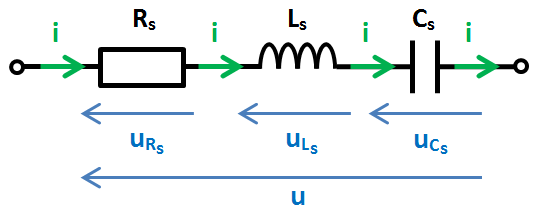
- une résistance Rs,
- une bobine Ls,
- un condensateur Cs. À titre d'exemple, nous prendrons des composants ayant les valeurs suivantes :
Rs = 40 Ω,
Ls = 1 mH (plus exactement 1,013 mH),
Cs = 100 pF. Ce circuit est parcouru par un courant sinusoïdal i de valeur maximale imax et de pulsation ω = 2πF, F étant la fréquence. uRs est la tension aux bornes de la résistance Rs. Cette tension est :
- sinusoïdale,
- de même pulsation ω donc de même fréquence F,
- en phase avec le courant i. Par conséquent, le déphasage de uRs par rapport à i est égal à 0° soit 0 radian. uLs est la tension aux bornes de la bobine Ls. Cette tension est :
- sinusoïdale,
- de même pulsation ω donc de même fréquence F,
- en quadrature avance par rapport au courant i. Par conséquent, le déphasage de uLs par rapport à i est égal à +90° soit +π/2 radian. uCs est la tension aux bornes du condensateur Cs. Cette tension est :
- sinusoïdale,
- de même pulsation ω donc de même fréquence F,
- en quadrature retard par rapport au courant i. Par conséquent, le déphasage de uCs par rapport à i est égal à −90° soit −π/2 radian. u est la tension aux bornes de l'ensemble RsLsCs.
On devrait pouvoir écrire : u = uRs + uLs + uCs puisque les trois composants sont en série. MAIS ces trois tensions uRs, uLs et uCs n'étant pas en phase, on ne peut absolument pas faire cette simple addition !
Par le calcul trigonométrique (et beaucoup plus facilement en utilisant les nombres complexes), on arrive à la formule suivante :
![]()
(1) 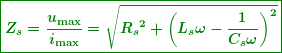
Il existe un moyen bien commode de la retrouver au moyen d'une construction géométrique simple appelée « diagramme de Fresnel ». 2. Obtention de l'impédance Zs au moyen du diagramme de Fresnel
Étape 1

Graduons cet axe en ohms (graduations non représentées sur le diagramme ci-dessus). La longueur OA représentera la valeur en ohms de la résistance Rs. Autrement dit OA = Rs. Étape 2
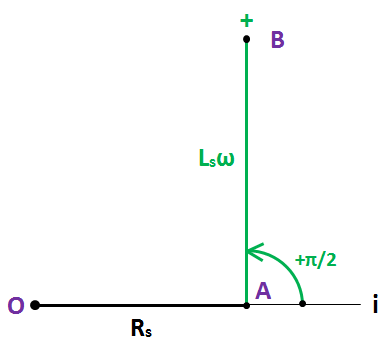
AB a donc tourné de +π/2 par rapport à la ligne i pour tenir compte du déphasage de uLs par rapport à i, déphasage valant justement +π/2 radian.
À l'étape précédente, nous avions positionné OA sur la ligne i car le déphasage de uRs par rapport à i était nul. Étape 3
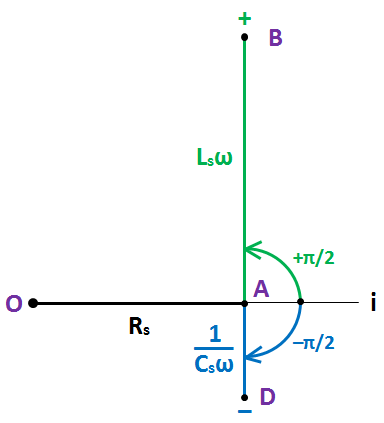
AD a donc tourné de −π/2 par rapport à la ligne i pour tenir compte du déphasage de uCs par rapport à i, déphasage valant justement −π/2 radian. Étape 4
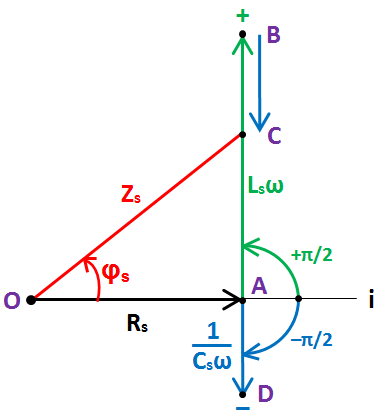
- de O à A pour Rs,
- de A à B pour Lsω, vers le haut,
- de B à C pour 1/(Csω), vers le bas. Avec la même échelle en ohms, l'impédance Zs du circuit RsLsCs série est égale à la longueur OC. Le triangle OAC est rectangle en A. Appliquons-lui le théorème de Pythagore : « Le carré de l'hypothénuse est égal à la somme des carrés des deux autres côtés », en rappelant que l'hypothénuse est le côté « qui regarde » l'angle droit, ici OC :
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[ \boxed{\boldsymbol{{{Z}_{s}}=\sqrt{{{{R}_{s}}^{2}+{{{\left( {{{L}_{s}}\omega -\frac{1}{{{{C}_{s}}\omega }}} \right)}}^{2}}}}}} \]](https://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-7a09902f48935c8fb5f886c53100bf53_l3.png)
1. Les calculs effectués ci-dessus l'ont été sur des longueurs de segments de droite et dans le cas où Lsω était plus grand que 1/(Csω).
2. Si au contraire Lsω est plus petit que 1/(Csω), nous obtenons le diagramme suivant :
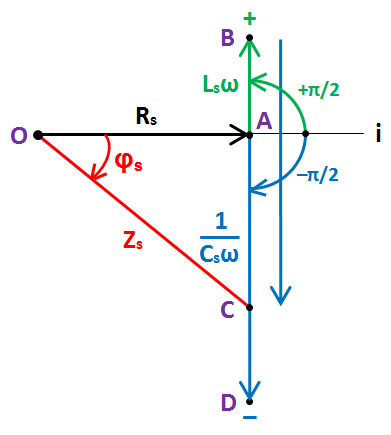
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[ \boxed{\boldsymbol{{{Z}_{s}}=\sqrt{{{{R}_{s}}^{2}+{{{\left( {{{L}_{s}}\omega -\frac{1}{{{{C}_{s}}\omega }}} \right)}}^{2}}}}}} \]](https://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-7a09902f48935c8fb5f886c53100bf53_l3.png)
Il existe une et une seule pulsation remarquable ω0s satisfaisant la condition suivante :
(2) ![]()
![]()
![]()
![]()
Dans notre exemple, la fréquence de résonance est égale à 500 kHz. Évolution de la fréquence de résonance quand on fait varier l'inductance Ls et/ou la capacité Cs
L'inductance Ls et la capacité Cs étant au dénominateur de la formule de Thomson, nous en déduisons immédiatement les comportements suivants :
- quand on augmente l'inductance Ls et/ou la capacité Cs, la fréquence de résonance diminue,
- quand on diminue l'inductance Ls et/ou la capacité Cs, la fréquence de résonance augmente. De plus l'inductance Ls et la capacité Cs apparaissant sous la forme de leur racine carrée, nous pouvons préciser (à titre d'exemples) :
- quand on multiplie par 4 l'inductance Ls ou la capacité Cs, la fréquence de résonance est divisée par 2,
- quand on divise par 4 l'inductance Ls ou la capacité Cs, la fréquence de résonance est multipliée par 2. Propriété fondamentale du circuit RsLsCs série à la fréquence de résonance
À la fréquence de résonance F0s et donc à la pulsation ω0s, la condition suivante est remplie :
![]()
![]()
![]()
Dans notre exemple, l'impédance est alors égale à 40 Ω. 4. Graphe de l'impédance Zs en fonction de la fréquence, allure générale
Il suffit de calculer l'impédance Zs pour différentes valeurs de la fréquence F en remplaçant dans l'expression (1) ω par 2πF. Il est souvent commode de tracer le graphe de Zs/Rs en fonction de F/F0s, F0s étant la fréquence de résonance :
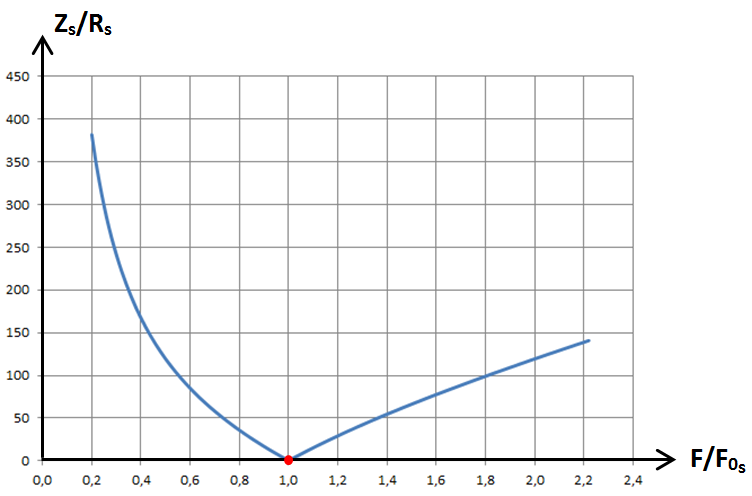
![]()
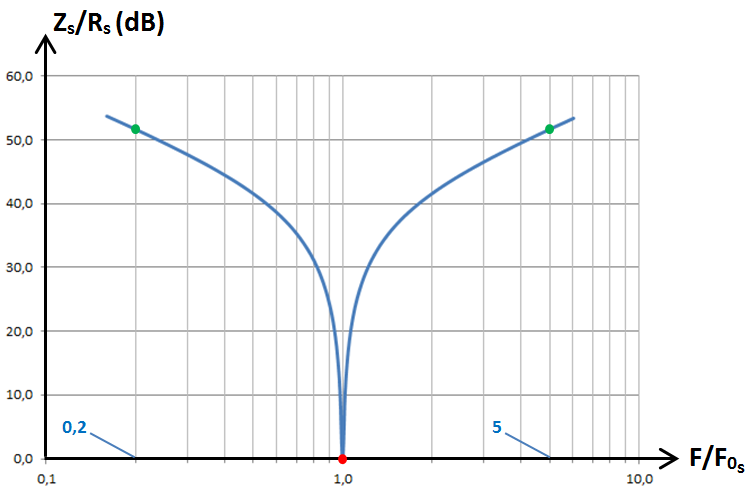
Supposons maintenant que la résistance Rs représente la résistance du fil de la bobine Ls. Attention : en régime sinusoïdal, il faut tenir compte de l'effet de peau qui augmente sensiblement la valeur de cette résistance !
Rappelons aussi que l'épaisseur de peau est inversement proportionnelle à la racine carrée de la fréquence (par exemple : quand la fréquence est multipliée par 4, cette épaisseur est divisée par 2). Voici la définition du « coefficient (ou facteur) de qualité » Qs de la bobine Ls :
![]()
(3) ![]()
![]()
Voici un zoom du graphe à proximité de la fréquence de résonance :
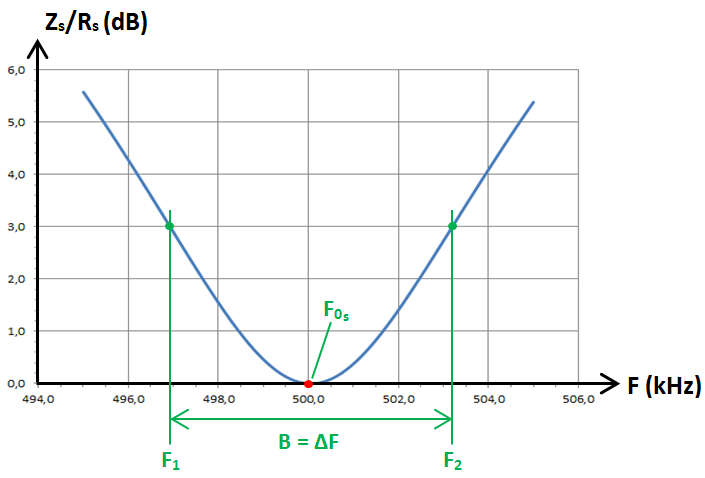
![]()
![]()
![]()
![]()
(4) ![]()
B = 6,3 kHz,
F1 = F0s − B/2 = 496,9 kHz,
F2 = F0s + B/2 = 503,2 kHz.
Nous retrouvons bien ces valeurs sur le graphe. Note : considérer que B se répartit par moitié de chaque côté de F0s n'est valable que si Q0s2 est très grand devant 1, ce qui est le cas dans notre exemple (79,6 × 79,6 = environ 6336). Influence de la valeur de Rs sur la largeur de bande
D'après la définition (3), plus la valeur de Rs est petite, plus le coefficient de qualité Q0s est élevé et d'après la formule (4), plus la largeur de bande B est étroite.
Remarquons que l'expression (4) peut s'écrire de la manière suivante :
![]()



