Formation à l'examen : décibels (1/2) - Radio-Club de Viry-Châtillon (91)

Formation à l’examen : décibels (1/2)

par F5FOD, Jean-Pierre Waymel

1. Le concept de « boîte noire »
De nombreux dispositifs électroniques présentent une entrée et une sortie :
- un amplificateur, microphone en entrée, haut-parleur en sortie,
- un poste de radio, antenne et terre en entrée, haut-parleur en sortie,
- un amplicateur, en général,
- un atténuateur,
- un filtre,
- et même une longueur de câble coaxial !

Pour les représenter dans leur globalité et vus de l'extérieur, on fait appel à des symboles géométriques simples comme des triangles, des carrés ou des rectangles. Ici, un rectangle, celui dessiné en traits pleins :

On ne se préoccupe pas des circuits électroniques présents dans le rectangle : c'est une « boîte noire ». On ne s'intéresse qu'à la fonction remplie par la boîte.
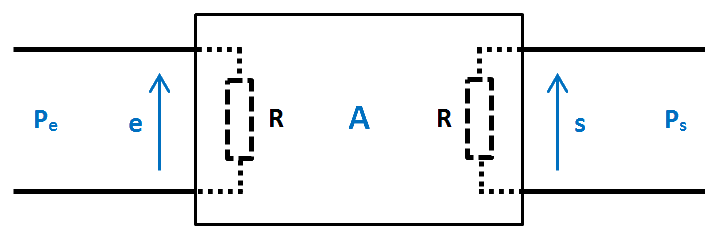
Notre boîte possède :
- un nom : A,
- une entrée sur deux fils, à gauche,
- une sortie sur deux fils, à droite.

Pe est la puissance appliquée à l'entrée de la boîte.
Ps est la puissance fournie par la boîte en sortie.

e est la tension appliquée à l'entrée de la boîte.
s est la tension fournie par la boîte en sortie.

Cas particulier
Les deux résistances dessinées en pointillés − car elles sont dans la boîte… et on ne devrait pas les voir − symbolisent :
- à gauche, la résistance que présente l'entrée de la boîte, c'est la « résistance d'entrée »,
- à droite, la résistance que présente la sortie de la boîte, c'est la « résistance de sortie ».
Pourquoi « cas particulier » ?
Tout d'abord parce qu'il s'agit de résistances pures, sans composante selfique L ni composante capacitive C. Ensuite, parce qu'elles ont la même valeur : R.

2. Gain en puissance
Le gain en puissance Gp de notre boîte noire s'exprime de la façon suivante :

(1) $\begin{equation*} \boxed{\boldsymbol{{{G}_{p}}=\frac{{{{P}_{s}}}}{{{{P}_{e}}}}}} \end{equation*}$

Très important : Gp est un nombre sans dimension (sans unité) puisqu'on divise des watts par des watts.

Si Ps = Pe, Gp = 1.
Si Ps > Pe, Gp > 1, nous avons affaire à un amplicateur de puissance.
Si Ps < Pe, Gp < 1, nous avons affaire à un atténuateur de puissance.

3. Gain en tension
Le gain en tension Gu de notre boîte noire s'exprime de la façon suivante :

(2) $\begin{equation*} \boxed{\boldsymbol{{{G}_{u}}=\frac{s}{e}}} \end{equation*}$

Très important : Gu est un nombre sans dimension (sans unité) puisqu'on divise des volts par des volts.

Si s = e, Gu = 1.
Si s > e, Gu > 1, nous avons affaire à un amplicateur de tension.
Si s < e, Gu < 1, nous avons affaire à un atténuateur de tension.

Comme nous ne nous intéresserons qu'à des signaux sinusoïdaux, il faudrait plutôt parler de module du gain, auquel cas e et s représentent respectivement les valeurs maximales des tensions sinusoïdales en entrée et en sortie.

4. Relation entre gain en tension et gain en puissance
Nous savons que la valeur efficace d'une tension sinusoïdale est égale à sa valeur maximale divisée par racine de 2. Nous pouvons donc écrire :

$\boldsymbol{{{P}_{s}}=\frac{{{{{\left( {{s}/{{\sqrt{2}}}\;} \right)}}^{2}}}}{R}}$

$\boldsymbol{{{P}_{e}}=\frac{{{{{\left( {{e}/{{\sqrt{2}}}\;} \right)}}^{2}}}}{R}}$

puis reporter ces expressions dans (1), ce qui donne :

$\boldsymbol{{{G}_{p}}=\frac{{\frac{{{{{\left( {{s}/{{\sqrt{2}}}\;} \right)}}^{2}}}}{R}}}{{\frac{{{{{\left( {{e}/{{\sqrt{2}}}\;} \right)}}^{2}}}}{R}}}=\frac{{{{{\left( {{s}/{{\sqrt{2}}}\;} \right)}}^{2}}}}{{{{{\left( {{e}/{{\sqrt{2}}}\;} \right)}}^{2}}}}=\frac{{{{s}^{2}}}}{{{{e}^{2}}}}={{\left( {\frac{s}{e}} \right)}^{2}}}$

Autrement dit, en utilisant l'expression (2) :

(3) $\begin{equation*} \boxed{\boldsymbol{{{G}_{p}}={{G}_{u}}^{2}}}} \end{equation*}$

5. Gain en puissance exprimé en décibels (dB)
Le gain en puissance peut également être exprimé en bels, de la façon suivante :

$\boldsymbol{G{}_{p}\textbf{ (bels)}=\log {{G}_{p}}=\log \left( {\frac{{{{P}_{s}}}}{{{{P}_{e}}}}} \right)}$

Mais il est préférable d'utiliser un sous-multiple : le décibel, dB en abrégé. D'où la nouvelle expression de ce gain en puissance :

(4) $\begin{equation*} \boxed{\boldsymbol{G{}_{p}\textbf{ (dB)}=10\times \log {{G}_{p}}=10\times \log \left( {\frac{{{{P}_{s}}}}{{{{P}_{e}}}}} \right)}} \end{equation*}$

Très important : le décibel n'est pas une unité de mesure !

6. « log » : qu'est-ce ?
« log » signifie « logarithme décimal ». Nous abrègerons ce nom et nous écrirons simplement « logarithme ».
Ce logarithme est une machine mathématique. On y entre un nombre a et il en sort un autre nombre : log(a) mais bien entendu pas n'importe quel nombre !
Traçons le graphe de log(a) en fonction de a :

En ce qui nous concerne, les caractéristiques principales de cette machine log(a) sont les suivantes :
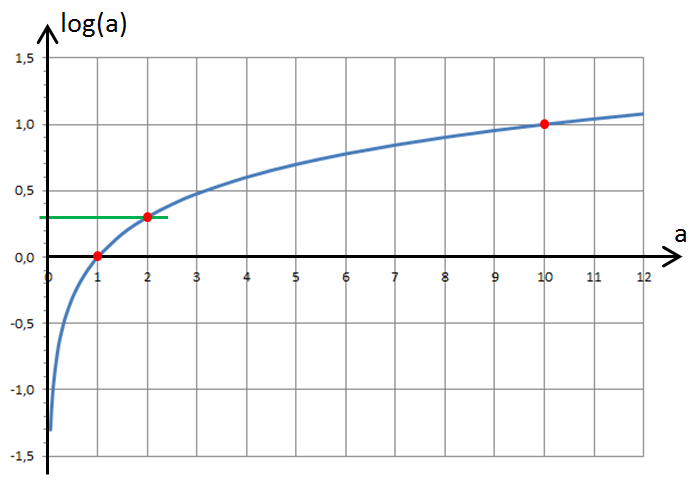
- le nombre a ne peut être ni négatif ni nul,
- si a se rapproche de 0, la valeur de log(a) devient très grande mais en négatif (log(a) est négatif et sa valeur absolue devient très grande),
- si a = 1, log(a) = 0,
- si a = 10, log(a) = 1.

Ce que l'on peut résumer par :
a > 0
log 1 = 0
log 10 = 1

Remarquons aussi :
- si a > 1, alors log(a) > 0
- si 0 < a < 1, alors log(a) < 0

7. Quelques valeurs remarquables du logarithme
log 1 = 0
log 2 = 0,3 (valeur arrondie)
log 3 = 0,5 (valeur arrondie)
log 5 = 0,7 (valeur arrondie)
log 10 = 1

8. Quelques propriétés fondamentales du logarithme
On n'a pas introduit le logarithme pour se compliquer les choses, bien au contraire.
La propriété la plus fondamentale est la transformation d'un produit en une somme :

(5) $\begin{equation*} \boxed{\boldsymbol{\log (a\times b)=\log (a)+\log (b)}} \end{equation*}$

Supposons que l'on ait deux nombres a et b possédant chacun de nombreux chiffres : faire leur produit a × b à la main donc sans calculette ni ordinateur serait très fastidieux et le résultat ne serait pas forcément exact !
Par contre, les « tables de log » fourniront les valeurs de log(a) et de log(b) dont la somme sera assez facile à faire avec beaucoup moins de risque d'erreur. Les mêmes tables de log fourniront ensuite le nombre dont le log sera égal au résultat de cette somme. Et ce nombre ne sera autre que la valeur du produit cherché : a × b !
C'est ainsi que procédaient les astronomes pour calculer les positions des corps célestes.
C'était aussi le principe de fabrication et de fonctionnement de la règle à calcul…
Quant à nous, les décibels, donc les logarithmes, seront bien utiles dans le domaine des filtres et amplificateurs, par exemple.

Calculons maintenant log(53) en utilisant la propriété (5) :

$\boldsymbol{\log ({{5}^{3}})=\log (5\times 5\times 5)=\log (5)+\log (5)+\log (5)=3\times \log (5)}$

c'est-à-dire :

$\boldsymbol{\log ({{5}^{3}})=3\log 5}$

Expression que nous pouvons généraliser sous la forme suivante :

(6) $\begin{equation*} \boxed{\boldsymbol{\log ({{a}^{b}})=b\log (a)}} \end{equation*}$

9. Gain en tension exprimé en décibels (dB)
Dans les conditions particulières indiquées (les résistances d'entrée et de sortie de notre boîte noire sont égales), en reprenant l'expression (3) et la propriété (6), nous pouvons écrire :

$\boldsymbol{\log {{G}_{p}}=\log ({{G}_{u}}^{2})=2\log {{G}_{u}}}$

Ou encore, en multipliant par 10 :

$\boldsymbol{10\log {{G}_{p}}=20\log {{G}_{u}}}$

On retrouve notre gain en puissance Gp exprimé en décibels.
Mais l'on a surtout pris l'habitude d'exprimer également en décibels le gain en tension Gu − en réalité le module du gain en tension − de la façon suivante (rappel : s et e sont des tensions maxi) :

(7) $\begin{equation*} \boxed{\boldsymbol{{{G}_{u}}\textbf{ (dB)}=20\times \log {{G}_{u}}=20\times \log \left( {\frac{s}{e}} \right)}} \end{equation*}$

Très important : à nouveau, le décibel n'est pas une unité de mesure !

10. Résumé important pour les gains exprimés en décibels (dB)
Pour les puissances, c'est le facteur 10 qui vient multiplier le log :

(8) $\begin{equation*} \boxed{\boldsymbol{{{G}_{p}}\textbf{ (dB)}=10\log \left( {\frac{{{{P}_{s}}}}{{{{P}_{e}}}}} \right)}} \end{equation*}$

Pour les tensions, c'est le facteur 20 qui vient multiplier le log.

(9) $\begin{equation*} \boxed{\boldsymbol{{{G}_{u}}\textbf{ (dB)}=20\log \left( {\frac{s}{e}} \right)}} \end{equation*}$

11. Quelques exemples
Rappels préalables

$\boldsymbol{\frac{1}{{{{a}^{n}}}}={{a}^{{-n}}}}$

D'où :

$\boldsymbol{0,5=\frac{1}{2}={{2}^{{-1}}} \qquad \frac{1}{8}=\frac{1}{{{{2}^{3}}}}={{2}^{{-3}}} \qquad 0,1=\frac{1}{{10}}={{10}^{{-1}}}}$

Rappelons également :

$\boldsymbol{\sqrt{a}={{a}^{{{1}/{2}\;}}}}$

D'où :

$\boldsymbol{\sqrt{2}={{2}^{{{1}/{2}\;}}}}$

Et enfin :

$\boldsymbol{\log 2\sim 0,3}$

Voici deux tableaux avec des valeurs usuelles que nous retrouverons par exemple en étudiant les filtres :

Gain en puissance

$\boldsymbol{{{{{P}_{s}}}}/{{{{P}_{e}}}}\;}$	$\boldsymbol{{{{{P}_{s}}}}/{{{{P}_{e}}}}\;\textbf{en dB}}$
1	$\boldsymbol{10\log 1=0\textbf{ dB}}$
2	$\boldsymbol{10\log 2=10\times 0,3=3\textbf{ dB}}$
0,5	$\boldsymbol{10\log \left( {{{2}^{{-1}}}} \right)=10\times (-1) \log 2=-3\textbf{ dB}}$
8	$\boldsymbol{10\log \left( {{{2}^{3}}} \right)=10\times 3\log 2=9\textbf{ dB}}$
1/8	$\boldsymbol{10\log \left( {{{2}^{{-3}}}} \right)=10\times (-3) \log 2=-9\textbf{ dB}}$
10	$\boldsymbol{10\log 10=10\textbf{ dB}}$
0,1	$\boldsymbol{10\log \left( {{{{10}}^{{-1}}}} \right)=-10\log 10=-10\textbf{ dB}}$

Gain en tension
Us = tension de sortie s.
Ue = tension d'entrée e.

$\boldsymbol{{{{{U}_{s}}}}/{{{{U}_{e}}}}\;}$	$\boldsymbol{{{{{U}_{s}}}}/{{{{U}_{e}}}}\;\textbf{en dB}}$
1	$\boldsymbol{20\log 1=0\textbf{ dB}}$
$\boldsymbol{\sqrt{2}}$	$\boldsymbol{20\log ({{2}^{{1/2}}})=20\times ({1}/{{2)}}\;\log 2=3\textbf{ dB}}$
$\boldsymbol{{1}/{{\sqrt{2}}}\;}$	$\boldsymbol{20\log ({{2}^{{-1/2}}})=20\times (-{1}/{{2)}}\;\log 2=-3\textbf{ dB}}$
2	$\boldsymbol{20\log 2=20\times 0,3=6\textbf{ dB}}$
0,5	$\boldsymbol{20\log \left( {{{2}^{{-1}}}} \right)=20\times (-1) \log 2=-6\textbf{ dB}}$
8	$\boldsymbol{20\log \left( {{{2}^{3}}} \right)=20\times 3\log 2=18\textbf{ dB}}$
1/8	$\boldsymbol{20\log \left( {{{2}^{{-3}}}} \right)=20\times (-3) \log 2=-18\textbf{ dB}}$
10	$\boldsymbol{20\log 10=20\textbf{ dB}}$
0,1	$\boldsymbol{20\log \left( {{{{10}}^{{-1}}}} \right)=-20\log 10=-20\textbf{ dB}}$