Radio-Club de Viry-Châtillon (91) - F5KEE

par F5FOD, Jean-Pierre Waymel

Résistance
Une résistance est un composant électronique opposant une certaine… résistance au passage du courant électrique. Tout étant affaire de quantité, on peut dire qu'un fil de cuivre est une résistance qui a une bien faible résistance !
Afin de distinguer le composant « résistance » de sa propriété de « résistance », il devrait être appelé « résistor ». Mais finalement ce terme est très peu utilisé.
En fait de métonymies, nous utiliserons également le même mot ou la même lettre pour désigner :
- une tension et sa valeur,
- ou un courant et sa valeur.

Exemple : le graphite
Nous avons vu comment le courant électrique pouvait circuler dans un conducteur comme le cuivre grâce à la particularité de l'électron unique présent sur la couche périphérique de chacun de ses atomes.
Avec le graphite, nous allons découvrir un type de conduction légèrement différent. Le graphite est l'une des variétés du carbone.
L'atome de carbone possède au total 6 électrons :
- 2 électrons sur la couche K,
- 4 électrons sur la couche L, sa dernière couche donc la couche périphérique. Le graphite est composé de feuilles de graphène, parallèles les unes aux autres.
Examinons une feuille de graphène :

La feuille a 2 dimensions. Les atomes de carbone sont disposés selon un motif hexagonal : ce sont les petits pois rouges du croquis ci-dessus. Et le motif se répète sur toute la feuille. Prenons l'exemple de l'atome « a ». Il est lié à 3 autres atomes : « b », « c » et « d ».
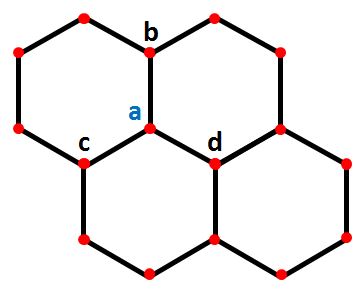
Comment s'effectue cette liaison ?
L'atome « a » partage un électron de sa couche périphérique avec l'atome « b », un autre avec l'atome « c » et encore un autre avec l'atome « d ». Par « partager un électron », il faut entendre « maintenir une liaison très forte ».
Au bout du compte, il ne lui reste plus qu'un seul électron non partagé sur sa couche périphérique. Cet électron va se comporter un peu comme l'électron solitaire du cuivre. Il va circuler dans le graphène si tant est qu'une source de tension puisse à terme l'attirer. Mais il se déplacera beaucoup moins facilement dans le graphène que dans le cuivre. De là prend naissance la fameuse « résistance ». Les feuilles de graphène (qui constituent le graphite) sont maintenues entre elles par une force faible. Ce qui explique au passage les propriétés lubrifiantes du graphite. Enfin, le graphène a des propriétés physiques assez extraordinaires mais qui n'entrent pas dans le champ de nos causeries. Et le diamant, qui est aussi du carbone ?
Oui, mais il n'existe que sous forme d'un réseau cristallin à 3 dimensions où chaque atome de carbone est lié à 4 autres atomes de façon à former 4 tétraèdres au sein d'un cube : tous les électrons périphériques sont mobilisés… et immobilisés, plus personne ne bouge ! Aucun électron ne peut se libérer pour circuler. Le diamant est donc un isolant. Sa structure explique aussi sa dureté.
La cristallographie étudie les structures cristallines des matériaux. Cette science n'entre pas non plus dans le champ de nos causeries… Néanmoins, les deux exemples cités, graphite et cuivre, nous ont permis d'avoir une petite idée de certains modes de circulation du courant dans la matière. Il y en a bien d'autres…

Connectons une résistance aux bornes d'un générateur de tension CC
Une résistance appelée R est maintenant connectée aux bornes d'une pile :

Si nous considérons que les fils de liaison ont une résistance nulle (fils parfaits), la tension E de la pile se retrouve aux bornes de la résistance R et un courant I traverse cette résistance.
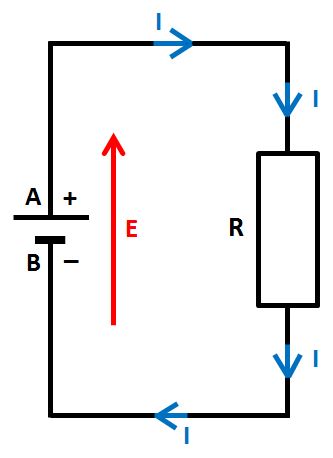
La valeur R de la résistance R (!) est obtenue par la formule suivante :

   

Une résistance s'exprime en ohms dont l'abréviation est "Ω".

Vérifions la tension aux bornes de la résistance R
Prenons une pile de 9 V.
Ne connectons pas tout de suite la résistance R : la pile est donc à vide, en circuit ouvert.
Une tension continue se mesure avec un « voltmètre pour tension continue », ce qui est logique !
Branchons donc un tel voltmètre « Voltm. » aux bornes de la pile de la façon suivante :
- le « + » du voltmètre sur le « + » de la pile,
- le « − » du voltmètre sur le « − » de la pile.
Ce qui correspond au schéma suivant :

Aucun courant ne traverse le voltmètre car nous avons pris soin d'utiliser un voltmètre « parfait » !
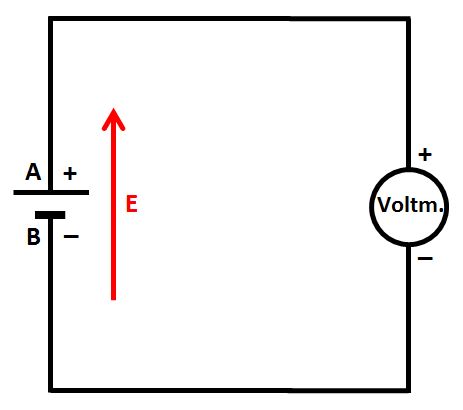
Malgré la présence de l'appareil de mesure, la pile est donc toujours en circuit ouvert.
Si le voltmètre est numérique, il affichera directement la valeur E.
Par exemple : E = 9,18 V.
Si nous inversons le sens de branchement du voltmètre, nous obtenons −9,18 V, ce qui est logique (se rappeler l'altitude de la mer par rapport au sommet du mont Blanc : −4810 m). Prenons maintenant une résistance R de 47 Ω et connectons-la :

Le voltmètre devrait toujours mesurer E donc 9,18 V.
Mais surprise, la tension mesurée par le voltmètre indique une valeur bien inférieure : environ 8,52 V.
Que se passe-il ?
Il se passe que la pile n'est pas un générateur de tension CC parfait, loin s'en faut. Son « imperfection » peut être représentée par une résistance « r » interne à la pile, d'où son nom de « résistance interne ». Cette résistance n'est pas un composant caché dans la pile. Il s'agit d'une image électrique de certains phénomènes électrochimiques qui s'y déroulent à l'intérieur même. Nous pouvons donc établir un nouveau schéma, plus conforme à la réalité :

Une pile est donc constituée :
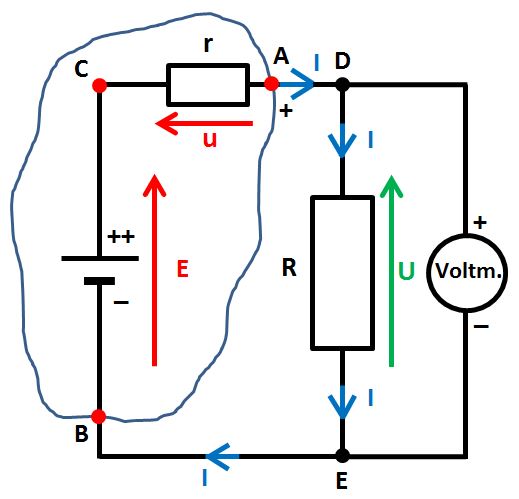
- d'un générateur délivrant une tension CC égale à E,
- « suivi » d'une résistance r représentant sa résistance interne.
La tension E est appelée « force électromotrice » de la pile ; en abrégé : « f.é.m. ».
Bien que le mot « force » apparaisse ici, l'unité de mesure est bien le volt.
Attention : le point C ou « ++ » n'est pas accessible !
La totalité de la pile est donc contenue dans le patatoïde du schéma. Ce schéma peut paraître bien compliqué mais nous allons le simplifier petit à petit. Déjà, comme les points A et D sont les mêmes électriquement parlant ainsi que les points B et E puisque les fils de liaison sont parfaits, nous pouvons le redessiner ainsi :

« + » et « − » sont les pôles de la pile tels que nous pouvons les voir… en regardant la pile ! Pour mettre en évidence certaines relations entre tensions, courants et résistances, il est souvent utile de redessiner un peu différemment telle ou telle partie d'un schéma. Bien entendu sans en modifier ses fonctionnalités.
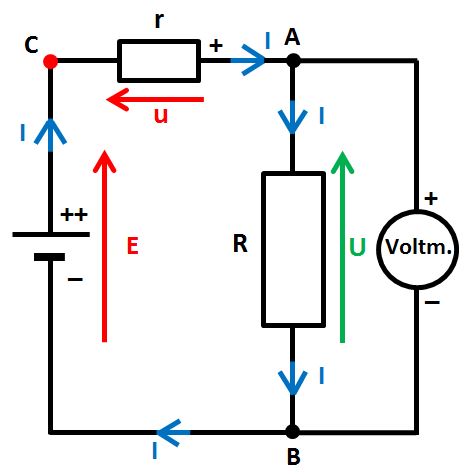
Par exemple :

Impact de la résistance interne du générateur de tension CC, loi d'Ohm
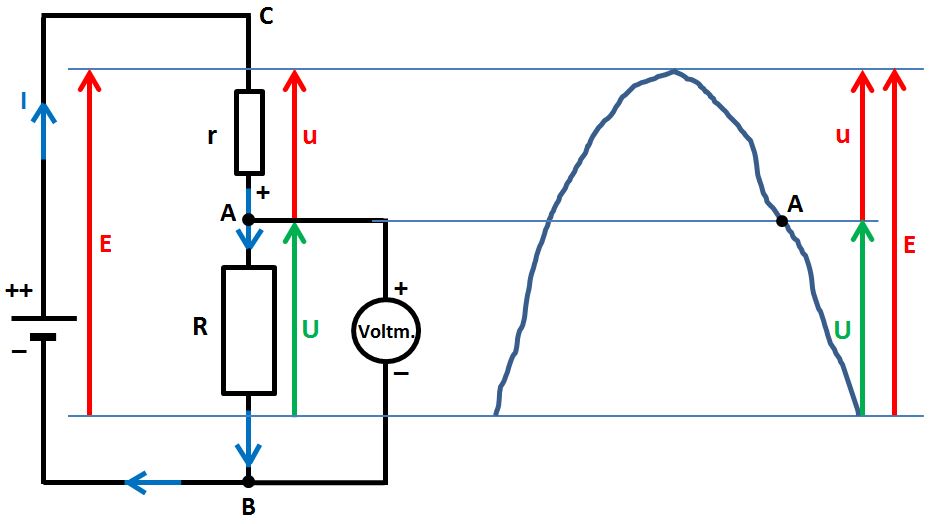
Ainsi dessiné, il apparaît clairement que la résistance interne r de la pile et notre résistance R se trouvent connectées « en série ». En effet, on dit que 2 résistances sont connectées en série quand elles sont reliées entre elles par une seule de leurs 2 extrémités, ce qui est le cas ici en A.
Le courant I traverse la résistance r puis la résistance R. Il n'y a toujours pas de courant dans le voltmètre puisqu'il est considéré comme parfait. La loi d'Ohm établit la relation suivante entre la valeur R d'une résistance, la valeur I du courant qui la traverse et la valeur U de la tension présente entre ses extrémités :

(1)  

… à condition de bien utiliser notre convention « tête-bêche » appliquée aux flèches du courant et de la tension à l'extérieur du générateur. Appliquons la loi d'Ohm à la résistance interne r ; u étant la tension aux bornes de r et I le courant qui la traverse, nous obtenons :

(2)  

Appliquons de même la loi d'Ohm à notre résistance R ; U étant la tension aux bornes de R et I le courant qui la traverse, nous obtenons :

(3)  

Reprenons maintenant l'analogie tension <=> altitude.
A est un refuge dans la montagne.
U est l'altitude de ce refuge par rapport au pied de la montagne. On pourrait parler aussi de dénivellation. Positive quand on monte, négative quand on descend, d'où l'importance de la bonne orientation de la flèche correspondante.
u est l'altitude du sommet par rapport au refuge… ou la dénivellation correspondante.
E est l'altitude du sommet par rapport au pied de la montagne. On voit tout de suite apparaître la relation suivante entre les altitudes ou les dénivellations, rien de bien savant :

   

Question tensions, pour nos 2 résistances en série, il en est exactement de même :

(4)  

Avec nos flèches bien orientées, les tension E, U et u sont toutes trois positives. Donc U est fatalement plus petit que E. On dit qu'il y a eu une « chute de tension » dans r et cette chute de tension est égale à u.
On ne retrouve donc pas « tout E » aux bornes de notre résistance R. C'est exactement ce que nous avions constaté lors de nos mesures. En effet, de l'expression (4), on déduit immédiatement (cf. la règle 5) :

   

ce qui est également « visible » sur le schéma.

Montage de résistances en série
Nous avons déjà vu 2 règles fondamentales :
- les tensions aux bornes de 2 résistances en série s'ajoutent (encore une fois : bien dessiner les flèches de tension dans le bon sens),
- les 2 résistances sont parcourues par un même courant.

En reportant dans (4) les expressions de U et u fournies respectivement par (3) et (2), nous obtenons (cf. la distributivité) :

   

donc :

(5)  

Tout se passe comme si, en lieu et place des 2 résistances R et r connectées en série, il n'y avait plus qu'une seule résistance dont la valeur serait égale à R + r. En effet, selon le schéma, cette résistance équivalente serait parcourue par le courant I et la tension à ses bornes serait égale à E. Ce qu'indique bien l'expression (5) qui n'est rien d'autre que la loi d'Ohm appliquée à cette résistance équivalente ! D'où la troisième règle fondamentale : connectées en série, les résistances s'ajoutent.

Le « bon » générateur de tension CC
Pour qu'un générateur de tension CC soit parfait, il faut que sa résistance interne soit nulle. Auquel cas, r = 0, ce qui entraîne u = 0 selon (2) puis U = E selon (4).
Dans notre exemple, on retrouverait alors entre les extrémités de la résistance R l'intégralité de la force électromotrice de la pile. Mais un tel générateur n'existe pas… Alors, quand peut-on dire que l'on a un « bon » générateur de tension CC ? L'expression (5) nous permet de calculer I (cf. la règle 4 et la règle 7) :

(6)  

En reportant cette expression de I dans (3), nous obtenons :

   

soit :

(7)  

Supposons que r vaille 1 Ω (il s'agit d'une autre pile que celle utilisée précédemment pour faire les 2 mesures de tension).
Si R = 1 Ω, alors U = (1/2) × E = 0,50 × E : on perd 50 % de E,
Si R = 10 Ω, alors U = (10/11) × E = 0,91 × E : on perd 9 % de E,
Si R = 100 Ω, alors U = (100/101) × E = 0,99 × E : on perd 1 % de E.
Autrement dit, si :

   

on retrouvera au moins 99 % de E aux bornes de R. Conclusion : un bon générateur de tension CC aura la plus faible résistance interne possible, en tout cas inférieure ou égale à 100 fois la résistance que l'on connectera à ses bornes.

Schéma normal et classique
Voici maintenant le schéma final, amplement suffisant pour effectuer tous les calculs et toutes les mesures :

Il est nettement plus simple que les schémas précédents qui n'avaient qu'un but explicatif sinon pédagogique dans la démarche choisie !

 << Causerie précédente Causerie suivante >>  << Retour à la table des matières