par F5FOD, Jean-Pierre Waymel
1. « Signal utile » et « signal porteur »Prenons l'exemple d'un émetteur radio en GO (Grandes Ondes), OM (Ondes Moyennes) ou OC (Ondes Courtes). Le « signal utile » que l'on veut transmettre est alors dans la plupart des cas du son, c'est-à-dire des paroles, de la musique. Il s’agit donc d’un signal BF (Basses Fréquences) destiné aux oreilles de l’auditeur.
Ce signal ne peut être transmis tel quel à grandes distances… heureusement, sinon on ne s’entendrait plus ! Il doit être « porté » par un autre signal qui, lui, sait franchir ces grandes distances. Ce « signal porteur » est un signal HF (Hautes Fréquences). 1.1 Expression du signal utile Su
Pour la parole par exemple, un microphone fournit le signal utile. On démontre (transformée de Fourier) que ce signal utile peut toujours être décomposé en signaux sinusoïdaux. Nous n'allons donc prendre qu'un seul signal sinusoïdal de fréquence Fu et de pulsation ωu = 2πFu. L’expression du signal utile Su peut alors se mettre sous la forme suivante :
![]()
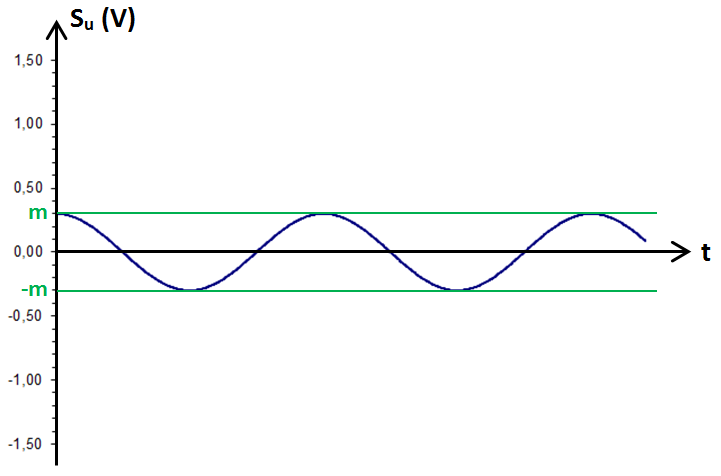
Le signal porteur est un signal sinusoïdal de fréquence Fp et de pulsation ωp = 2πFp. L’expression du signal porteur Sp peut alors se mettre sous la forme suivante :
![]()
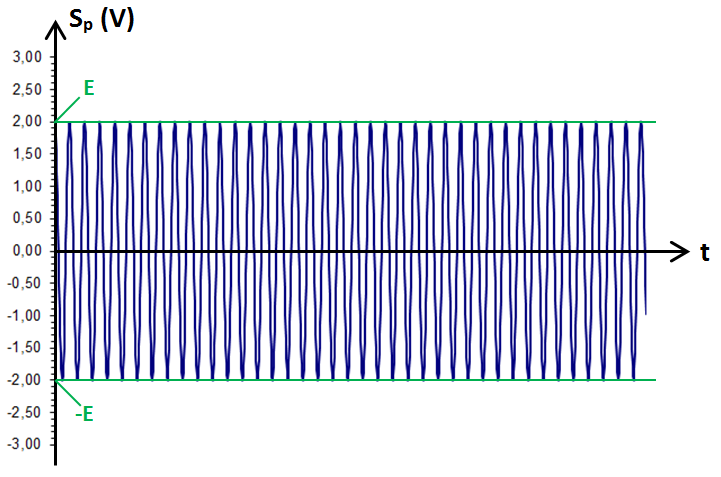
L’idée est de faire varier la valeur de E au rythme du signal utile. Le signal utile Su va donc « moduler l'amplitude » du signal porteur Sp. Nous réaliserons ainsi une « modulation » et cette modulation sera appelée « Modulation d'Amplitude (MA) » ou « Amplitude Modulation (AM) », en anglais. En modulation d'amplitude, le signal utile n'est pas forcément un signal BF. Par contre, la condition suivante doit être respectée :
![]()
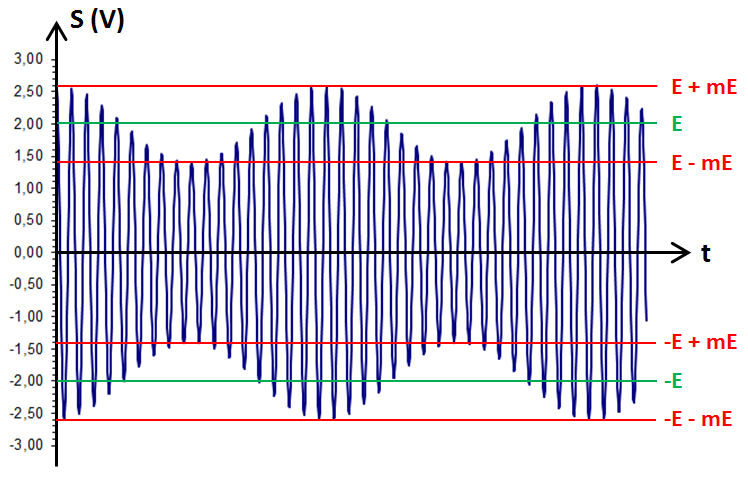
E + mE = 2 + 0,3 × 2 = 2,6 V
E − mE = 2 − 0,3 × 2 = 1,4 V
−E + mE = −2 + 0,3 × 2 = −1,4 V
−E − mE = −2 − 0,3 × 2 = −2,6 V 3. Le modulateur en modulation d'amplitude
Comment faire pour obtenir un signal répondant au graphe précédent ?
Voici l'une des méthodes utilisées :
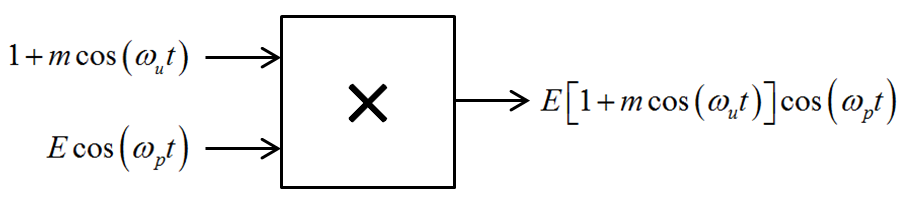
- première tension en entrée :
- seconde tension en entrée :
(1) ![]()
![]()
Le multiplieur de tensions ne fournit pas des volts au carré mais des volts ! Dans l'expression (1), le terme m n'est plus qu'un simple coefficient sans dimension. Il est alors appelé « indice », « taux » ou « profondeur » de modulation. 4. Amplitudes maximales et minimales de S
Amplitudes maximales
Maxi le plus positif
Quand
Maxi le moins positif
Quand
Mini le moins négatif
Quand
Mini le plus négatif
Quand
Voici un moyen extrêmement simple permettant de calculer l'indice de modulation m à partir de ce graphe :
(2) ![]()
Développons l'expression (1) :
(3) ![]()
Rappelons alors cette relation trigonométrique :
![]()
![]()
![]()
![]()
- un signal à la fréquence
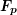 et d'amplitude maximale
et d'amplitude maximale 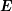 , c'est le signal porteur,
, c'est le signal porteur, - un signal à la fréquence
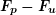 et d'amplitude maximale
et d'amplitude maximale 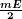 ,
, - un signal à la fréquence
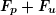 et d'amplitude maximale
et d'amplitude maximale 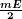 .
.
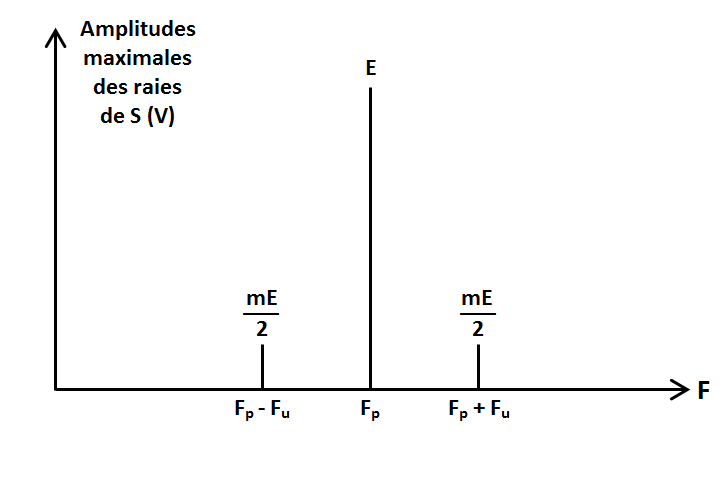
Bien entendu le signal utile ne se réduit pas à la seule fréquence Fu mais s’étale d’une fréquence minimale Fu_min à une fréquence maximale Fu_max. Voici alors comment peut se présenter le spectre du signal modulé en amplitude :
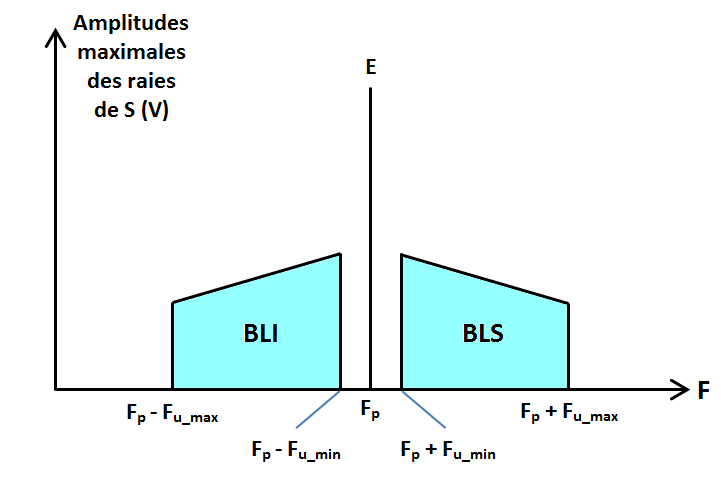
- « bande » parce que les fréquences incluses dans cette bande occupent une « largeur » donnée du « spectre radioélectrique »,
- « latérale » parce chaque bande voisine la fréquence porteuse,
- « inférieure » quand les fréquences comprises dans la bande sont inférieures à Fp, « supérieure » quand les fréquences comprises dans la bande sont supérieures à Fp. Très important : l'information contenue dans chaque bande est identique. La bande latérale inférieure (BLI) s’étend de (Fp − Fu_max) à (Fp − Fu_min).
La bande latérale supérieure (BLS) s’étend de (Fp + Fu_min) à (Fp + Fu_max).
Le signal S est composé de ces deux bandes latérales et de la fréquence porteuse centrale Fp. Il occupe une largeur totale en fréquence égale à (Fp + Fu_max) − ( Fp − Fu_max) = 2 × Fu_max. Autrement dit, plus Fu_max est grande, plus cette largeur totale est grande.
En GO où Fu_max = 4500 Hz, elle est égale à 9000 Hz. Pour Europe 1 en GO :
- la fréquence porteuse Fp est égale à 183 kHz,
- la BLI démarre à 178,5 kHz (183 − 4,5),
- la BLS s’étend jusqu’à 187,5 kHz (183 + 4,5).
La station occupe donc la portion suivante du spectre radioélectrique : 178,5 à 187,5 kHz. Pour ne pas se brouiller l’une l’autre, les fréquences porteuses de deux stations adjacentes doivent donc être distantes d'au moins 9 kHz. 8. Quelques remarques
- Les BLI et BLS contenant strictement la même information utile, la station émettrice occupe par conséquent deux fois trop de spectre ! Or le spectre des fréquences est une ressource non extensible…
- La fréquence porteuse, plus simplement appelée « porteuse », n’est finalement pas nécessaire puisqu’elle ne contient aucune information utile. Notons que la BLI et/ou la BLS ayant des fréquences élevées pourront quand même être transmises à de longues distances au cas où la porteuse serait supprimée.
- L’émetteur gaspille de l’énergie pour envoyer dans son antenne cette porteuse et une bande latérale superflue (la BLI ou la BLS). 9. Contrôle du signal modulé en amplitude S
On choisit une valeur de fréquence utile Fu, par exemple 600 ou 1000 Hz.
Le contrôle du signal modulé en amplitude s'effectue de manière classique à l'oscilloscope : Y(t) et l'on obtiendra un oscillogramme conforme au graphe présenté en paragraphe 2. L'expression (2) permettra de calculer la valeur de m.
Le contrôle peut également s'effectuer avec un analyseur de spectre et l'on obtiendra un spectrogramme conforme au graphe présenté en paragraphe 6. Méthode du trapèze
Cette troisième méthode utilise l'oscilloscope en mode Y(X) et non plus en mode Y(t). On applique toujours le signal à contrôler S à l'entrée Y (« entrée verticale »). Par contre, on applique maintenant le signal utile Su ou ici (1 + Su) à l'entrée X (« entrée horizontale ») qui n'est donc plus l'axe du temps comme précédemment :
![]()
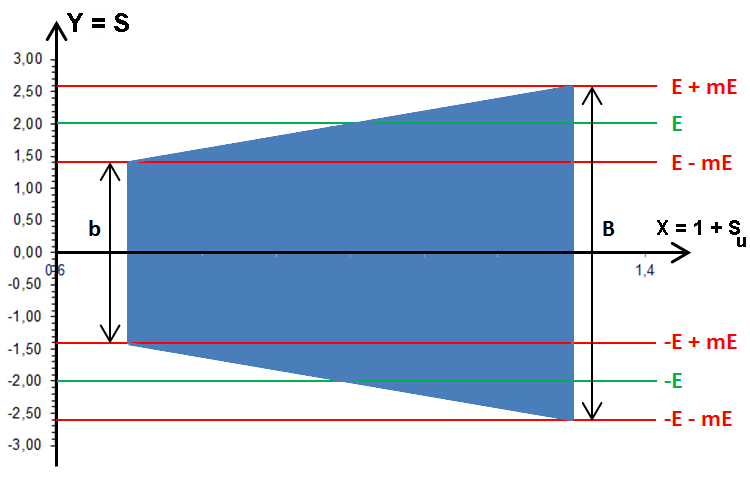
![]()
Quand m est supérieur à 1, il y a « surmodulation ». Cette surmodulation provoquera de la distorsion et rendra l'écoute difficile à la réception. Voici ce que devient le graphe du signal S pour m = 1,3 :
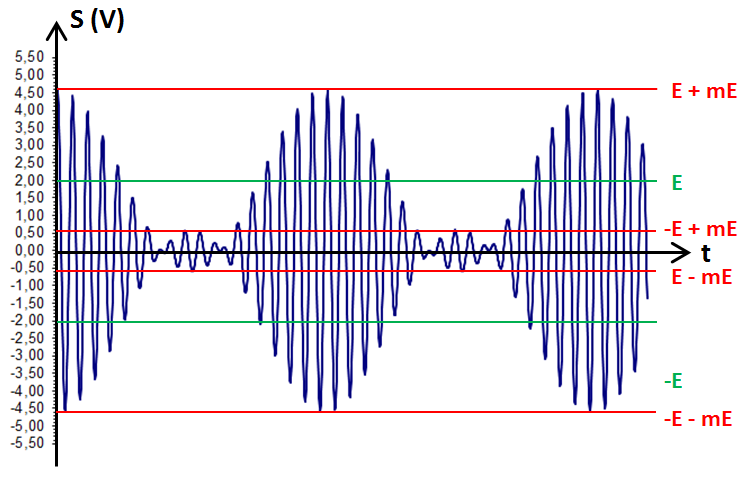
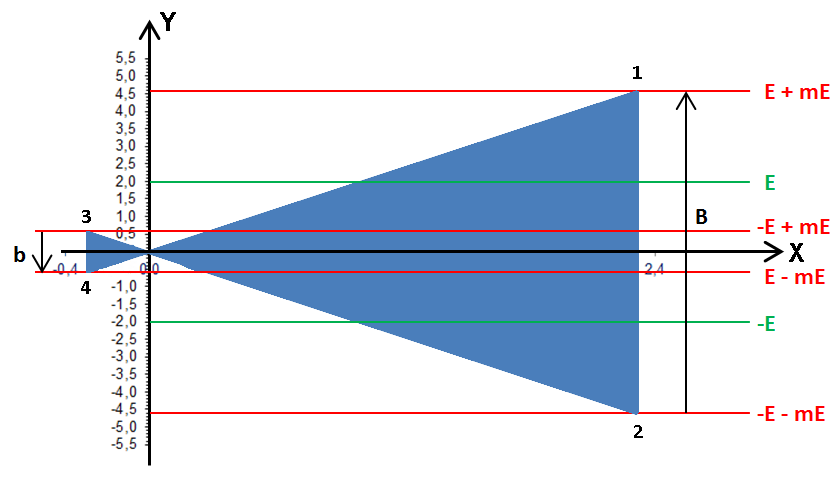
![]()
Reprenons l'expression (1) et faisons entrer E dans la partie entre crochets :
![]()
![]()
![]()
![]()
![]()
Observons de plus près ce terme A. C'est une tension qui est elle-même la somme des deux tensions suivantes :
- une tension continue (constante) : E,
- une tension sinusoïdale : mEcosBF. Reprenons les mêmes valeurs :
m = 0,3
E = 2 V
donc mE = 0,6 V
et traçons le graphe de E en fonction du temps :

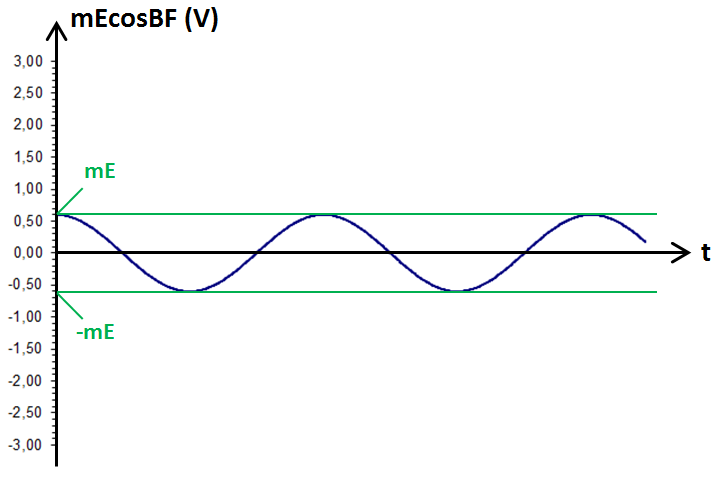
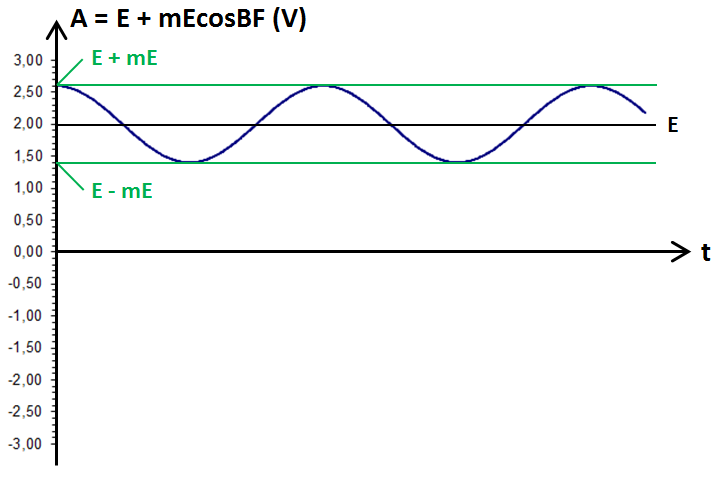
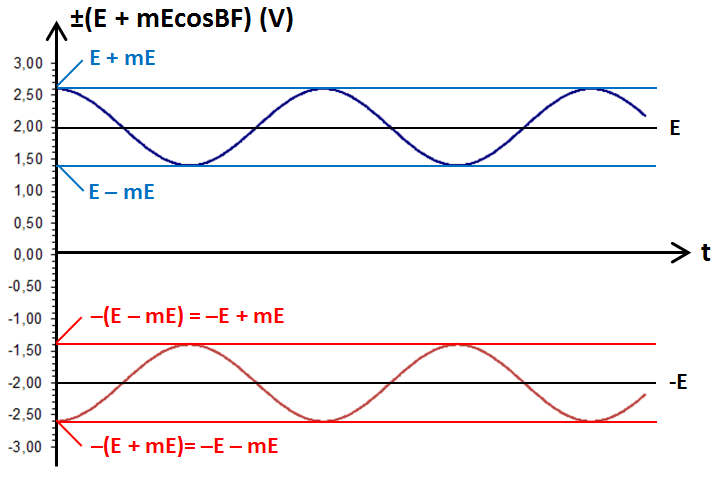
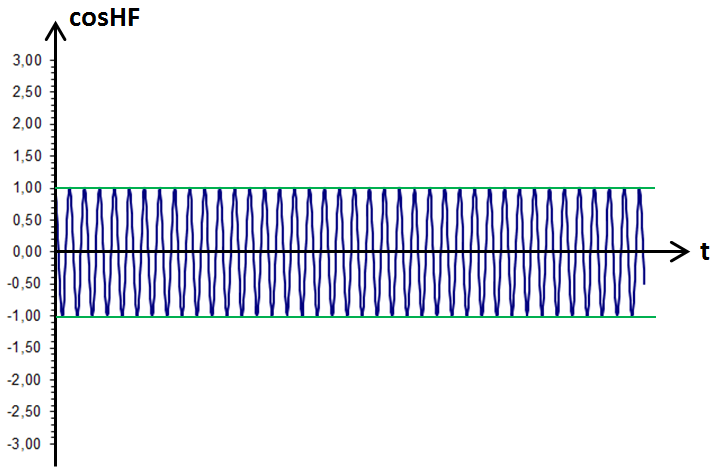
Si on multiplie ce cosinus par A, c'est-à-dire par (E + mcosBF), cette valeur maximale passe de +1 à +1 × (E + mcosBF) et évolue donc comme (E + mcosBF).
Tandis que sa valeur minimale passe de −1 à −1 × (E + mcosBF) et évolue comme −(E + mcosBF).
Autrement dit, S = AcosHF va venir s'inscrire entre les deux courbes bicolores tracées précédemment et finalement nous obtiendrons ce graphe :
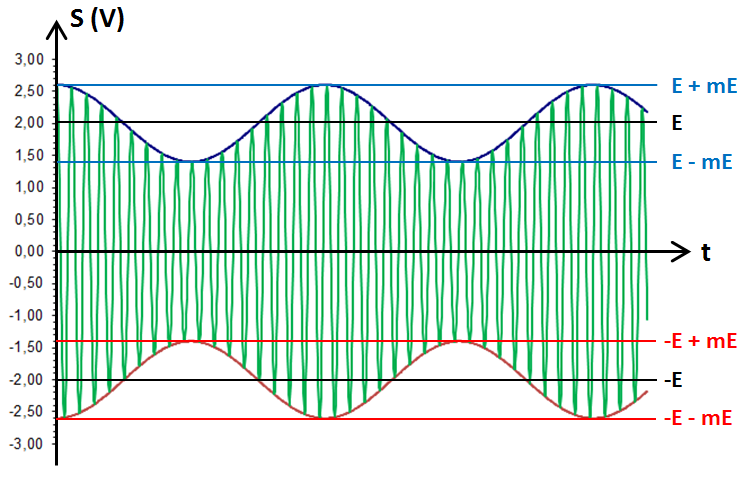
Nous retrouvons donc bien notre signal : une porteuse HF modulée en amplitude par un signal utile BF. << Causerie précédente Causerie suivante >> << Retour à la table des matières
