Radio-Club de Viry-Châtillon (91) - F5KEE

par F5FOD, Jean-Pierre Waymel

Angles : degrés et radians
Les angles peuvent se mesurer en degrés mais également en radians, abréviation : « rad ».
En physique, c'est le radian qui est utilisé. Les angles sont orientés : ils sont comptés positivement si l'on tourne dans le sens contraire des aiguilles d'une montre. Un quart de tour de cadran correspondant à un angle droit.
Et un angle droit vaut 90°.
« 90° » est égal à π/2 radian :

Un demi-tour de cadran correspond à un angle plat.
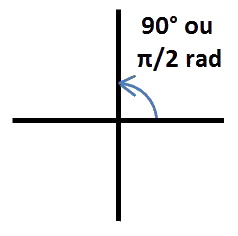
Et un angle plat vaut 2 × 90° soit 180°.
« 180° » est donc égal à 2 × (π/2) soit π radians :

Trois quarts de tour de cadran valent 3 × 90° soit 270°.
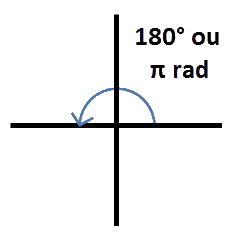
« 270° » est donc égal à 3 × (π/2) soit 3π/2 radians :

Un tour complet de cadran vaut 4 × 90° soit 360°.
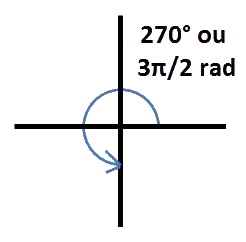
« 360° » est donc égal à 4 × (π/2) soit 2π radians :

… Et 0 tour de cadran vaut 0° soit 0 radian :

Attention : 0 tour de cadran n'est pas égal à un tour complet de cadran !

Vitesses
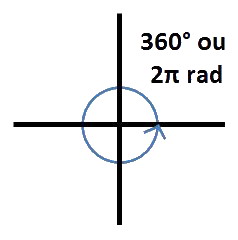
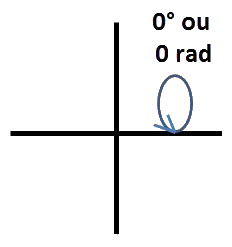
En ligne droite
Un mobile M se déplace en ligne droite de A à B à vitesse constante égale à v.
Un tel mouvement est appelé « mouvement rectiligne uniforme » :

Le temps mis par le mobile M pour effectuer le parcours AB est égal à t et ce parcours a une longueur égale à d (« d » pour « distance »).
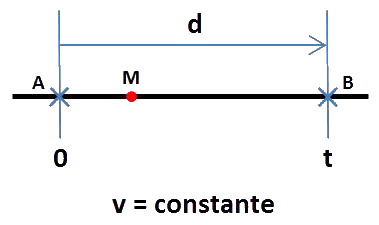
La relation qui lie d, v et t est la suivante :

(1)  

On en déduit immédiatement cette autre relation :

(2)  

et celle-ci :

(3)  

Il est d'ailleurs facile de vérifier ces deux dernières relations en pratiquant sur chacune d'entre elles le produit en croix.

Sur un cercle
Maintenant le mobile M se déplace sur un cercle de centre O et de rayon OM :

Il part de A, tourne dans le sens contraire des aiguilles d'une montre pour retourner en A après avoir effectué un tour complet.
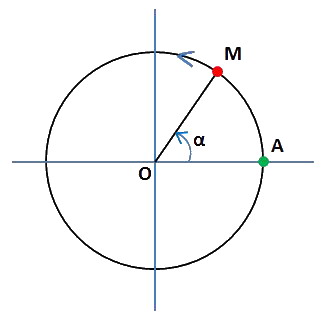
L'angle α parti d'une valeur nulle au départ en A atteint donc 360° au retour en A (tour complet) soit 2π radians. Au lieu de calculer la distance parcourue comme précédemment, nous pouvons calculer l'angle α balayé à chaque instant t de la façon suivante :

(4)  

où ω est « la vitesse angulaire ».
Si α est exprimé en degrés, ω le sera en degrés par seconde.
Si α est exprimé en radians, ω le sera en radians par seconde. À partir de (4), on obtient la relation suivante :

(5)  

et celle-ci :

(6)  

Il est d'ailleurs facile de vérifier ces deux dernières relations en pratiquant sur chacune d'entre elles le produit en croix. Application (vitesse angulaire)
Supposons que la vitesse angulaire ω soit constante et qu'il faille 20 ms pour que M fasse un tour complet soit 2π radians.
Nous pouvons alors calculer cette vitesse en utilisant la relation (5) :

   

Si le point M continue de tourner, son mouvement deviendra un mouvement périodique de période T égale à 20 ms, par définition de la période.
La fréquence F, égale à 1/T, vaudra alors 1/0,020 = 50 Hz.

Génération d'un signal sinusoïdal
Reprenons notre point M qui tourne sur un cercle et le même exemple de vitesse angulaire constante : 100 π.
C'est-à-dire qu'un tour complet durera 20 ms.
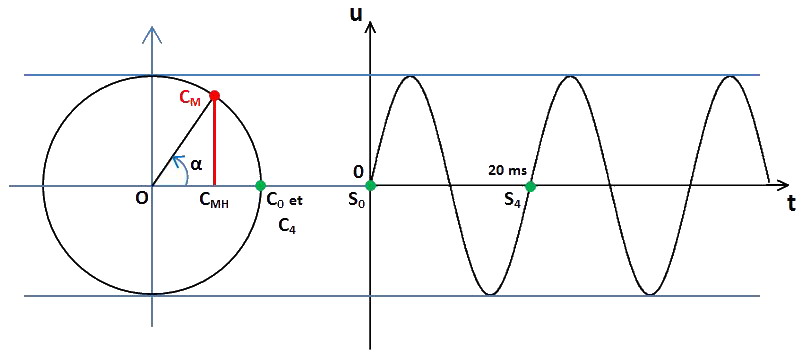
Ce point M sera maintenant appelé CM pour bien indiquer qu'il est sur le Cercle :

Traçons la perpendiculaire à l'axe horizontal OC0 issue de CM.
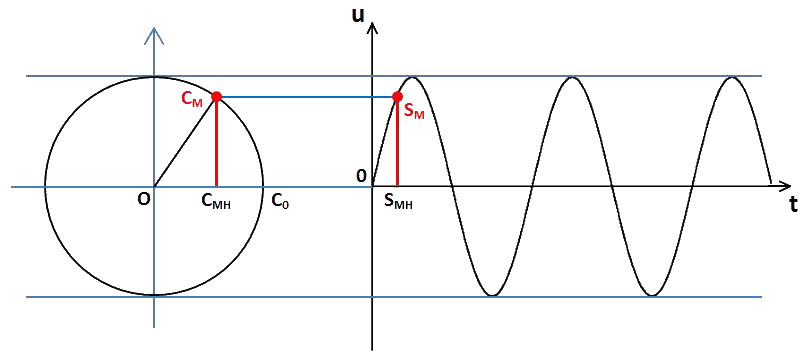
Elle coupe cet axe horizontal en CMH.
Ce point CMH est appelé « projection orthogonale » de CM sur la droite OC0. Sur le graphe de droite, nous reporterons la longueur CMHCM en SMHSM (« S » comme Sinusoïde) au bon endroit, comme nous le décrirons un peu plus loin. Pour l'instant, intéressons-nous à quelques points bien spécifiques.

À t = 0 ms

CM est en C0.
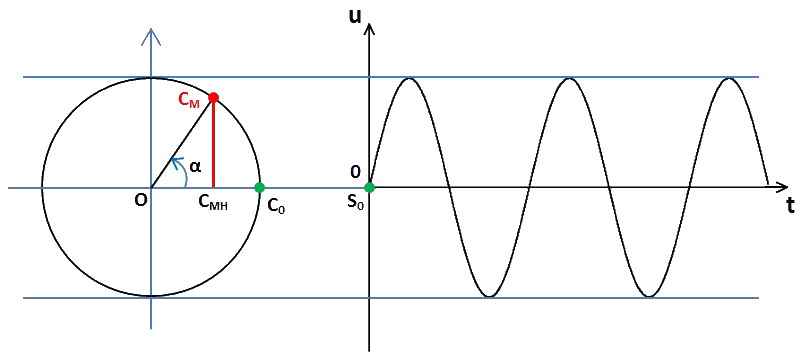
Le point C0H est alors confondu avec C0 (le point C0H étant la projection orthogonale de C0 sur la droite OC0).
Le segment CMHCM n'est donc plus qu'un point : sa longueur est nulle. Sur le graphe de droite, le point correspondant à C0 est le point S0, marquant la même amplitude verticale u nulle au même temps t = 0 ms.

À t = 5 ms

En 5 ms, le point CM arrive en C1 car 5 = 20/4 => 5 ms est le temps nécessaire à CM pour parcourir un quart de tour depuis C0.
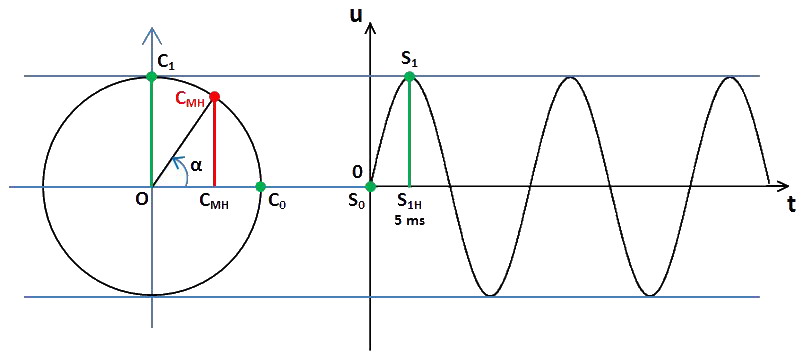
Le point C1H est alors confondu avec O (le point C1H étant la projection orthogonale de C1 sur la droite OC0).
Le segment C1HC1 est donc identique au segment OC1 et sa longueur est égale au rayon du cercle. Sur le graphe de droite, le point correspondant à C1 est le point S1, la longueur S1HS1 étant égale au rayon du cercle, au même temps t = 5 ms qui est égal à T/4.

À t = 10 ms

En 10 ms, le point CM arrive en C2 car 10 = 20/2 => 10 ms est le temps nécessaire à CM pour parcourir la moitié du tour depuis C0.
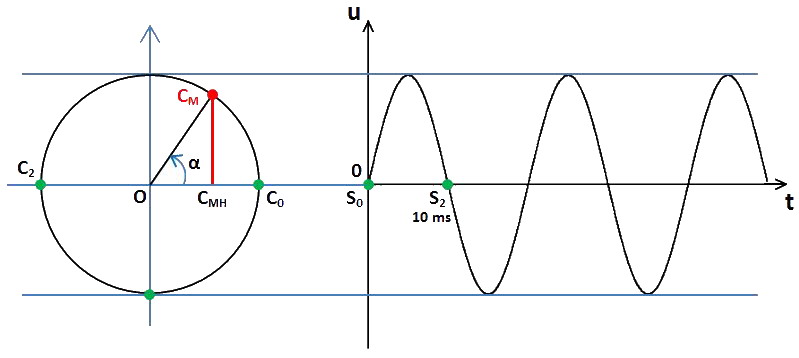
Le point C2H est alors confondu avec C2 (le point C2H étant la projection orthogonale de C2 sur la droite OC0).
Le segment CMHCM n'est donc plus qu'un point : sa longueur est nulle. Sur le graphe de droite, le point correspondant à C2 est le point S2, marquant la même amplitude verticale u nulle au même temps t = 10 ms qui est égal à T/2.

À t = 15 ms

En 15 ms, le point CM arrive en C3 car 15 = 20× (3/4) => 15 ms est le temps nécessaire à CM pour parcourir trois quarts de tour depuis C0.
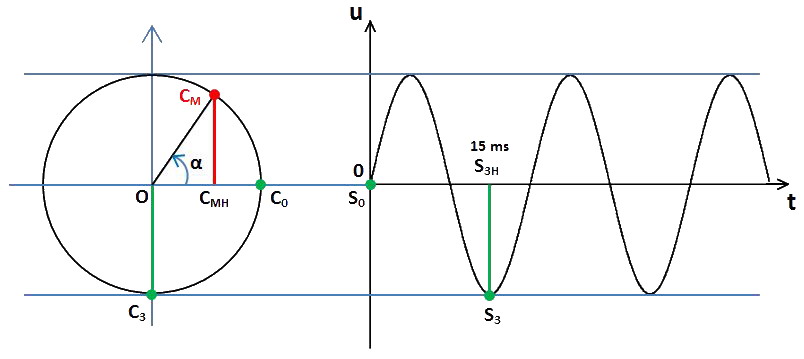
Le point C3H est alors confondu avec O (le point C3H étant la projection orthogonale de C3 sur la droite OC0).
Le segment C3HC3 est donc identique au segment OC3 et sa longueur est égale au rayon du cercle. Sur le graphe de droite, le point correspondant à C3 est le point S3, la longueur S3HS3 étant égale au rayon du cercle, au même temps t = 15 ms qui est égal à 3T/4.
Les axes verticaux étant orientés, S3 est bien d'amplitude u négative, d'où sa position.

À t = 20 ms

En 20 ms, le point CM arrive en C4 car 20 ms est le temps nécessaire à CM pour parcourir un tour complet depuis C0.
Le point C4H est alors confondu avec C4 (le point C4H étant la projection orthogonale de C4 sur la droite OC0).
Le segment CMHCM n'est donc plus qu'un point : sa longueur est nulle. Sur le graphe de droite, le point correspondant à C4 est le point S4, marquant la même amplitude verticale u nulle au même temps t = 20 ms qui est égal à T.

Pour tous les points intermédiaires

Pour un point CM quelconque sur le cercle, commençons par mesurer l'angle α avec un rapporteur.
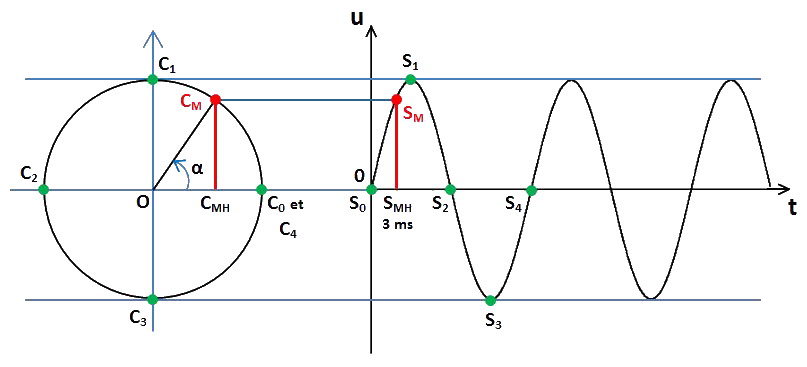
Ici nous obtenons 55°.
Convertissons les degrés en radians, sachant que « 180° » équivaut à π radians :

   

soit environ 0,96 rad.

Et calculons le temps nécessaire à CM pour arriver à cet endroit du cercle.
Comme nous connaissons la vitesse angulaire ω (100π rad/s), utilisons l'expression (6) pour calculer ce temps :

   

soit environ 3 ms.

Sur le graphe de droite, à t = 3 ms, durée représentée par le segment S0SMH, nous pouvons donc placer SM avec SMHSM = CMHCM.

En procédant ainsi sur de multiples valeurs de l'angle α, nous verrons se dessiner un beau signal sinusoïdal de période T égale à 20 ms.
Il faudra bien reporter en amplitudes négatives les points SM correspondant aux points CM du cercle dont l'angle α est compris entre π et 2π.

Résumé
Quand le point CM effectue un tour de cercle en T secondes, le point SM décrit une sinusoîde, plus exactement une période de sinusoïde.

Pulsation d'un signal sinusoïdal
En reprenant la relation (4) avec α = 2π et t = T, nous obtenons 2π = ω × T soit :

(7)  

Et comme T = 1/F, nous avons :

   

soit :

(8)  

Cette expression sera capitale pour la suite de nos causeries.
En électronique, ω est appelé « pulsation ».

Conclusion
Un alternateur est en quelque sorte une machine qui transforme la longueur du segment orienté CMHCM en une tension électrique sinusoïdale !
Et nous n'avons rien fait d'autre que de construire la courbe mathématique de Asin(ωt) en fonction du temps t, A étant le rayon du cercle…

En effet, la définition de est la suivante (petit développement mathématique non au programme) :

   

Comme et comme est le rayon du cercle, nous pouvons écrire :

   

soit :

   

Remarque importante
A est aussi la valeur crête de notre sinusoïde.
Si A = 1 (volt ou ampère) :
- la valeur maximale de u est égale à +1,
- la valeur minimale de u est égale à −1.

 << Causerie précédente Causerie suivante >>

 << Retour à la table des matières