Lignes de transmission : modélisation
par F5FOD, Jean-Pierre Waymel
Prenons un petit tronçon de ligne :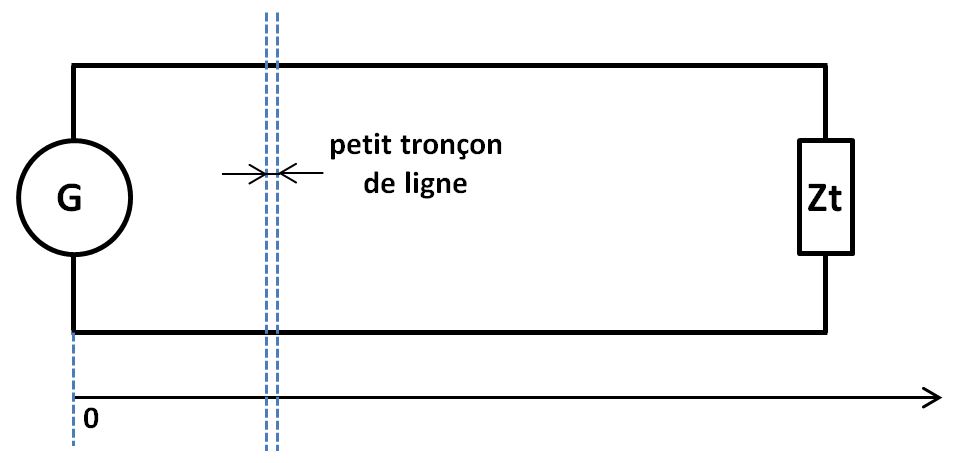
Ce tronçon est compris entre les deux lignes pointillées verticales.
Étirons ces deux lignes verticales pour mieux voir :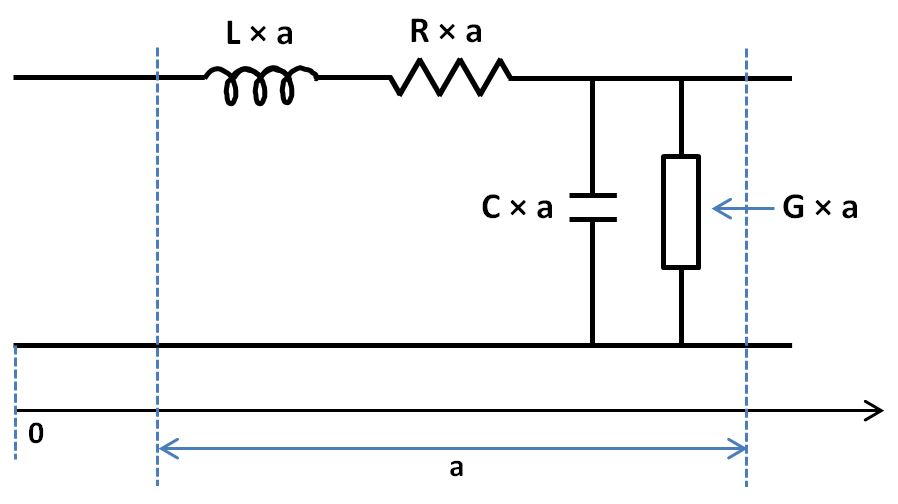
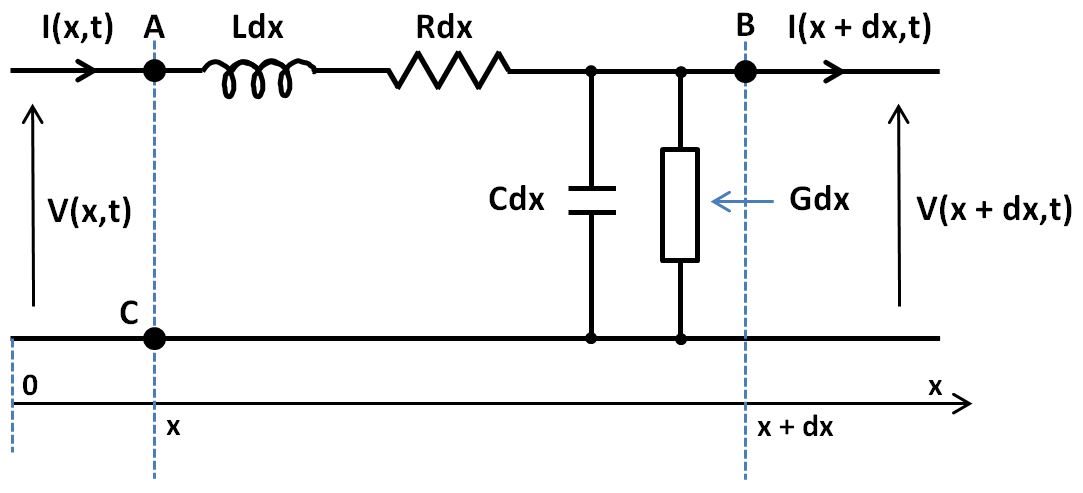
Dans chaque petit tronçon de ligne :
- la self représente les effets magnétiques dus au passage du courant dans les fils (un bout de fil, c'est une spire étirée !),
- deux fils « qui se voient » (bien qu'il y ait un diélectrique entre eux) constituent un condensateur,
- ces fils présentent une résistance non nulle,
- entre ces deux fils, il y a des pertes dans le diélectrique (ce dernier pouvant être de l'air, du polyéthylène, du PTFE, etc.).
Pourquoi L, C, R et G sont-ils multipliés par "a", la longueur du petit tronçon de ligne ?
Parce que L, C, R et G sont respectivement l'inductance, la capacité, la résistance et la conductance (pertes diélectriques) linéiques, c'est-à-dire par unité de longueur.
Donc par mètre.
Par conséquent, L s'exprime en H/m, C en F/m, R en Ω/m et G en Ω-1/m.
Pour "a" mètres, l'inductance, par exemple, vaut L × a.
Cette façon de modéliser une ligne n'est valable que si a est très petit devant la longueur d'onde du signal fourni par le générateur G. Elle permet d'établir l'équation dite « équation des télégraphistes ».
L'équation des télégraphistes
Tension et courant dans la ligne varient selon l'emplacement choisi sur la ligne et selon le temps. Leurs valeurs sont régies par l'équation des télégraphistes.
De nombreux mathématiciens et physiciens ont œuvré à l'élaboration et à la résolution de cette équation différentielle. Citons Sir William Thomson (1824-1907), Gustav Kirchhoff (1824-1887), Oliver Heaviside (1850-1925), Henri Poincaré (1854-1912) et Émile Picard (1856-1941).
Jean Mawhin a publié un excellent article à ce sujet :
Henri Poincaré et l'équation des télégraphistes.
Nous nous contenterons plus tard du régime sinusoïdal et bien souvent, nous considèrerons la ligne sans pertes.
<suite>
.
Le générateur G est situé à
.
.
,
c'est-à-dire selon l'emplacement choisi sur la ligne et selon le temps.
.
le courant qui entre en A.
.
.![\[ \boldsymbol{V(x,t)=Ldx\frac{{\partial I(x,t)}}{{\partial t}}+RdxI(x,t)+V(x+dx,t)} \]](https://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-37d8a45033c2832a99de4be22324d3b5_l3.png "Rendered by QuickLaTeX.com")
![\[ \boldsymbol{-\frac{{V(x+dx,t)-V(x,t)}}{{dx}}=L\frac{{\partial I(x,t)}}{{\partial t}}+RI(x,t)} \]](https://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-866b7cf432388b55c3053950c6c240fe_l3.png "Rendered by QuickLaTeX.com")
![\[ \boldsymbol{I(x,t)=Cdx\frac{{\partial V(x+dx,t)}}{{\partial t}}+GdxV(x+dx,t)+I(x+dx,t)} \]](https://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-be24d812ea9c34f6bd8b11faf5f7c81e_l3.png "Rendered by QuickLaTeX.com")
![\[ \boldsymbol{-\frac{{I(x+dx,t)-I(x,t)}}{{dx}}=C\frac{{\partial V(x+dx,t)}}{{\partial t}}+GV(x+dx,t)} \]](https://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-a6f25788e0d148a295b786d03ca17180_l3.png "Rendered by QuickLaTeX.com")
![\[ \boldsymbol{-\frac{{\partial I(x,t)}}{{\partial x}}=C\frac{{\partial V(x+dx,t)}}{{\partial t}}+GV(x+dx,t)} \]](https://www.f5kee.fr/wp-content/ql-cache/quicklatex.com-42b51f7c53a8fe47ecc5b1e335ad4ffb_l3.png "Rendered by QuickLaTeX.com")
sans approximation du premier ordre si l'on dessinait sur le schéma l'ensemble C parallèle G à l'entrée du tronçon et l'ensemble L série R à sa sortie.
